백준 2042 (구간 합 구하기) c++

문제

2042번: 구간 합 구하기

n개의 숫자를 차례대로 입력받고 m번의 수 변경이 일어나고 k번의 구간의 합을 구하는 문제입니다.

a가 1이면 b번째 수 위치를 c로 바꾸고

a가 2이면 b부터 c 구간의 합을 구하면 됩니다.

따라서 총 m+k번의 쿼리가 진행 됩니다.

 

단순히 prefix sum으로 해결하기에는 수를 계속 해서 바꿔주는 과정이 있기 때문에 더 효율적인 시/공간 복잡도로

이루어진 자료구조가 필요합니다.

 

따라서 Segment Tree 자료구조를 이용하여 수를 update하는 연산에 O(log n) + 구간의 합을 구하는 연산 O(log n)의

시간 복잡도로 문제를 해결하였습니다.

 

Segment Tree의 핵심 아이디어는 길이가 x인 특정 구간을 log x개의 부분 구간으로 나누어서 합을 구하는 것입니다.

길이가 8인 배열에서 2^0인 구간들로만 나누어져 있습니다.

2^1 인 구간에서는 2^0인 두 구간의 합이 저장됩니다.

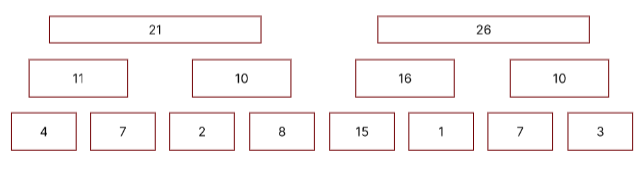
마찬가지로 2^2 인 구간을 구하였습니다.

마지막으로 2^3 인 구간들을 저장하였습니다.

 

이를 구현하기 위해서는 각각의 구간들을 이진트리 형태로 만들어야 합니다. 

이는 보통 배열로 구현합니다. 

배열로 구현하기 때문에 최종 루트노드의 index는 1로 만듭니다.

루트노드의 왼쪽 자식은 루트노드의 index * 2 , 오른쪽 자식은 루트노드의 index * 2 + 1 로 만듭니다.

우리는 구간합 뿐만 아니라 update 연산까지도 구현을 하여야 합니다.

세그먼트 트리는 이진트리 이므로 트리의 높이는 최대 log N 이기 때문에 최대 시간복잡도는 O(log N) 입니다.

예를 들어 2번쨰 원소를 update 하려면 빨간색 노드들만 다 바꿔주면 됩니다.

---

init 함수(top-down 방식)

ll init(ll N, ll s, ll e) {
    if (s == e)return tree[N] = arr[s];
    ll mid = (s + e) / 2;
    return tree[N] = init(N * 2, s, mid) + init(N * 2 + 1, mid + 1, e);
}

주어진 수를 segment tree로 초기화 해주는 작업입니다.

첫번째 인자 N은 tree의 index번호 입니다. top-down방식이므로 처음에 시작할때 N은 1입니다.

두번째 인자 s는 구간의 시작점, e는 구간의 끝점입니다.

---

query 함수(top-down 방식)

ll query(ll N, ll s, ll e, ll l, ll r) { //[l, r] 의 구간합을 구하는 과정
    if (l > e || r < s)return 0; //구간에 들어가 있지 않을 경우
    if (l <= s && e <= r)return tree[N]; //구간 합에 들어 왔을 때
    ll mid = (s + e) / 2;
    return query(N * 2, s, mid, l, r) + query(N * 2 + 1, mid + 1, e, l, r);
}

구간합을 구해주는 함수입니다. 

l과 r은 구간합을 구할려는 구간의 시작점과 끝점입니다. 

따라서 재귀함수가 계속해서 진행해도 변하지 않습니다.

---

update 함수(top-down 방식)

void update(ll N, ll s, ll e, ll idx, ll val) {
    if (idx > e || idx < s)return;//바꿀려는 위치가 구간에 없을 경우
    if (s == e) {
        if (idx == s)tree[N] = val;
        return;
    }
    ll mid = (s + e) / 2;
    update(N * 2, s, mid, idx, val);
    update(N * 2 + 1, mid + 1, e, idx, val);
    tree[N] = tree[N * 2] + tree[N * 2 + 1];
}

idx위치에 있는 있는 수를 val로 update해주는 함수입니다.

3~6 번째 줄은 update하는 과정이고 

10번째 줄은 update된 tree들을 다시 새로 update하는 과정입니다.

---

전체 코드입니다.

#include<iostream>
#include<algorithm>
#include<climits>
#include<string>
#include<vector>
#include<queue>
#include<stack>
#include<deque>
#include<cmath>
#include<time.h>
#include<cstring>
#include<cmath>
#include<cstring>
#include<limits>
using namespace std;
using ll = long long;
using ull = unsigned long long;
ll tree[10000000], arr[1000001];
ll n,m,k;
ll a, b, c;
ll init(ll N, ll s, ll e);
ll query(ll N, ll s, ll e, ll l, ll r);
void update(ll N, ll s, ll e, ll idx, ll val);
int main() {
    ios_base::sync_with_stdio(false), cin.tie(NULL), cout.tie(NULL);
    cin >> n >> m >> k;
    for (int i = 0; i < n; i++)cin >> arr[i];
    init(1, 0, n - 1);
    m += k;
    while (m--) {
        cin >> a >> b >> c;
        if (a == 1)update(1, 0, n - 1, b - 1, c);
        else cout << query(1, 0, n - 1, b - 1, c - 1) << '\n';
    }
    return 0;
}
ll init(ll N, ll s, ll e) {
    if (s == e)return tree[N] = arr[s];
    ll mid = (s + e) / 2;
    return tree[N] = init(N * 2, s, mid) + init(N * 2 + 1, mid + 1, e);
}
ll query(ll N, ll s, ll e, ll l, ll r) { //[l, r] 의 구간합을 구하는 과정
    if (l > e || r < s)return 0; //구간에 들어가 있지 않을 경우
    if (l <= s && e <= r)return tree[N]; //구간 합에 들어 왔을 때
    ll mid = (s + e) / 2;
    return query(N * 2, s, mid, l, r) + query(N * 2 + 1, mid + 1, e, l, r);
}
void update(ll N, ll s, ll e, ll idx, ll val) {
    if (idx > e || idx < s)return;//바꿀려는 위치가 구간에 없을 경우
    if (s == e) {
        if (idx == s)tree[N] = val;
        return;
    }
    ll mid = (s + e) / 2;
    update(N * 2, s, mid, idx, val);
    update(N * 2 + 1, mid + 1, e, idx, val);
    tree[N] = tree[N * 2] + tree[N * 2 + 1];
}