백준 2188 (축사 배정) c++

문제

2188번: 축사 배정

source와 sink를 만들고, source로 부터 소들로 용량이 1인 간선을 잇고, 축사에서 sink로 용량이 1인 간선들을

이어 줍니다.

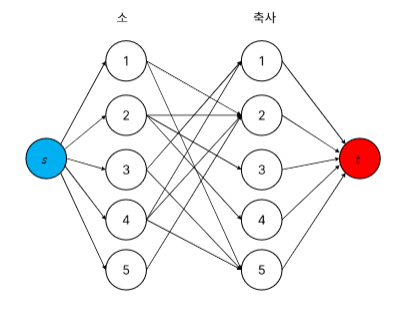
s -> t로 가는 maximal flow를 구하는 것과 동치인 문제입니다.

소를 최대한 축사로 배정하는 것과 s에서 t로 최대한 많은 유량을 흘리는 것과 동치입니다.

    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        int a, b;
        cin >> a;
        for (int j = 0; j < a; j++) {
            cin >> b;
            add_edge(i, b + n, 1);
        }
    }
    for (int i = 1; i <= n; i++)add_edge(0, i, 1); //soruce
    for (int i = 1; i <= m; i++)add_edge(i + n, n + m + 1, 1);//sink
    
 
void add_edge(int from, int to, int c) {
    v[from].push_back(to);
    v[to].push_back(from);
    cap[from][to] = c;
    //backward edge의 경우 흐르는 유량만큼이 용량이 됩니다.
    //하지만 흐르는 유량이 0이므로 그대로 0입니다.
}

주어진 정보를 입력 받습니다.

따라서 다음과 같은 간선 연결을 완료 하였습니다.

cap[from][to] 배열은 간선의 용량을 표시한 것입니다. (forward edge)

축사에는 1마리의 소만 들어갈 수 있으므로 간선의 용량들은 모두 1입니다.

backward edge는 현재 흐르는 유량이 없으므로 0입니다. 따라서 따로 표시는 안해줍니다.

10번째 줄은 source(0) 에서 모든 소의 노드에 간선을 이어주는 역할을 합니다.

11번째 줄은 축사에서 sink(11)로 간선을 이어주는 역할을 합니다.

---

이제 간선을 이어줬으므로 flow알고리즘을 적용해서 문제를 해결하겠습니다.

알고리즘은 Edmond-Karp알고리즘을 사용하여 bfs방식을 적용하였습니다.

cout << Edmond_Karp(0, n + m + 1);
 
 
int Edmond_Karp(int source, int sink) {
    int max_flow = 0;
    while (1) { //augmenting path가 없을때까지 반복, bfs로 진행
        queue<int>q;
        q.push(source);
        memset(cache, -1, sizeof(cache));
        cache[source] = 0;
        while (q.size()) {
            int cur = q.front();
            q.pop();
            for (auto nxt : v[cur]) {
                if (cache[nxt] == -1 && cap[cur][nxt] - flow[cur][nxt] > 0) {
                    cache[nxt] = cur;//직전에 어디서 왔는지 저장
                    q.push(nxt);
                    if (nxt == sink)break;
                }
            }
        }
        if (cache[sink] == -1)break; //현재 residual graph에서 sink로 가는 간선이 없음
        int min_cap = 1e9;
        //현재 residual graph 용량의 최솟값을 min_cap에 저장
        for (int i = sink; i != source; i = cache[i]) {
            int bef = cache[i];
            min_cap = min(min_cap, cap[bef][i] - flow[bef][i]);
        }
        max_flow += min_cap;
        //유량을 min_cap 만큼 흘리므로 residual graph를 수정
        for (int i = sink; i != source; i = cache[i]) {
            int bef = cache[i];
            flow[bef][i] += min_cap;
            flow[i][bef] -= min_cap;
        }
    }
    return max_flow;
}

먼저 함수의 인자로 source와 sink가 들어갑니다.

5번째 줄 max_flow 변수에는 간선의 최소유량을 계속해서 반복적으로 흘리는데 

흘리는 유량의 누적합을 저장하기 위한 변수입니다. 마지막에 return을 하게 되면 정답이 됩니다.

while (1) { //augmenting path가 없을때까지 반복, bfs로 진행
        queue<int>q;
        q.push(source);
        memset(cache, -1, sizeof(cache));
        cache[source] = 0;
        while (q.size()) {
            int cur = q.front();
            q.pop();
            for (auto nxt : v[cur]) {
                if (cache[nxt] == -1 && cap[cur][nxt] - flow[cur][nxt] > 0) {
                    cache[nxt] = cur;//직전에 어디서 왔는지 저장
                    q.push(nxt);
                    if (nxt == sink)break;
                }
            }
        }
        

코드를 좀더 자세히 살펴보겠습니다.

3번째 줄을 보면 먼저 시작은 sink로 부터 시작하므로 큐에 넣어 줍니다.

 

4 -5 째 줄을 보면 cache[] 배열이 있는데 캐시 메모리 처럼 이전에 있었던 노드의 위치를 저장하기 위함입니다.

예를 들어 cache[1] = 0 (1번 노드가 이전에 있었던 노드 = 0번 노드)

모든 cache배열을 -1로 설정해둡니다. 만약 cache배열이 -1이 아니면 이미 연결된 다른 노드가 있다는 의미입니다.

 

6번째 줄 while절 부터 이제 bfs를 실행합니다.

 

7번째 줄 cur에는 현재 큐에 들어간 sink, 0이 들어가 있습니다. 

 

9-13 번째 줄은 augmenting path를 찾아줄 것입니다.

 

9번째 줄을 보면 이제 v[0]에 들어가있는 모든 노드들을 탐색할 것입니다.

0번째 노드와 연결되있는 노드들은 1, 2, 3, 4, 5 입니다.

 

10번째 줄을 보면 cache[nxt] = -1 즉, 다음에 갈 노드가 현재 어떤 노드와도 연결이 되어있지 않아야 합니다.

cap[cur][nxt] - flow[cur][nxt] >0 즉, forward edge가 진행할려면  항상 용량 - 유량이 양수 이여야하기 때문입니다.

현재  아직 유량을 흘러보내지 않았으므로 모든 유량은 0입니다.

 

11번째 줄을 보면 연결된 노드가 어디서 왔는지 cache배열에 저장됩니다. 

0번 노드로 부터 1번 노드 부터 탐색할 것이므로 cache[1] = 0 입니다.

 

13번째 줄을 보면 nxt = sink라는 것은 augmenting path를 찾았다는 의미입니다. 따라서 멈처주면 됩니다.

위의 코드들을 다 실행하면 위와 같은 그림처럼 됩니다.

augmenting paht는 0 -> 1 -> 7 -> 11 입니다.

이제 augmenting path에서 최소 용량을 찾아 최소용량만큼 유량을 흘려줄것입니다.

---

if (cache[sink] == -1)break; //현재 residual graph에서 sink로 가는 간선이 없음
int min_cap = 1e9;
        //현재 residual graph 용량의 최솟값을 min_cap에 저장
for (int i = sink; i != source; i = cache[i]) {
    int bef = cache[i];
    min_cap = min(min_cap, cap[bef][i] - flow[bef][i]);
}
max_flow += min_cap;
//유량을 min_cap 만큼 흘리므로 residual graph를 수정
for (int i = sink; i != source; i = cache[i]) {
    int bef = cache[i];
    flow[bef][i] += min_cap;
    flow[i][bef] -= min_cap;
}
    

1번째 줄을 보면 cache[sink]가 -1이라는 것은 augmenting path를 못찾았다는 의미 이기 때문에 break 해줍니다.

현재 cache[sink] = 7입니다.

 

이제 augmenting path들을 탐색하면서 가장 용량이 작은 값을 min_cap에다가 저장할 것입니다.

 

4번째 줄을 보면 sink부터 시작해서 거꾸로 탐색할 것입니다. 

cache[sink] = 7

cache[7] = 1

cache[1] = source

 

6번째 줄을 보면 cap[bef][i] - flow[bef][i] 간선의 용량을 의미합니다. min함수를 사용해 계속해서 용량의 

최솟값을 찾아줍니다.

 

8번째 줄을 보면 augmenting path에서 찾은 용량의 최솟값을 max_flow에 누적해서 더해줍니다.

 

10번째 줄을 보면 이제 min_cap 만큼의 유량을 흘러 보냈으므로 residual graph를 수정해줘야 합니다.

 

12번째 줄을 보면 bef에서 i로 흘러간 유량을 의미합니다. min_cap 많큼 흘려 줬으므로 min_cap만큼 더해줍니다.

 

13번째 줄을 보면 i에서 bef로 흘러간 유량을 의미합니다. 유량이 반대쪽으로 흘러갔으므로 min_cap만큼 빼줍니다.

원래 유량이 0이 었으므로 그래도 0입니다.

검은색 선은 용량을 의미합니다. cap[][]

빨간색 선은 흘러간 유량을 의미합니다. flow[][]

파란색선 또한 흘러간 유량을 의미합니다. flow[][]

---

여기까지 끝냈다는 의미는 1번째 소가 7번째 축사로 들어갔다는 의미입니다.

결국 다시 while절을 반복하여도  1번째 노드와 7번째 노드를 건드릴 수 없습니다.

 

다시 while절부터 시작해서 augmentiong path를 찾으면 

위의 그림과 같습니다. 0 -> 2 -> 8 -> 11

0 -> 1 -> 7 -> 11은 건드릴 수 없습니다.(용량 - flow 가 0이기 때문)

이러한 과정을 반복하면 maximal flow를 찾을 수 있습니다.

---

위의 문제는 이분매칭으로도 해결이 가능합니다.

이분매칭은 flow를 활용하는 문제에도 적용이 가능하고 O(VE)의 시간복잡도를 가지며 maximal flow보다

구현이 쉽고 빠르다는 장점이 있습니다.

이분 매칭은 dfs를 활용하여 문제를 해결합니다.

vector<int>v[410];
bool checked[1010];
int d[1010]; //점유하고 있는 노드의 정보

벡터 v에는 노드와 간선의 정보가 들어가게 됩니다.

checked 배열에는 dfs를 진행하면서 왼쪽 노드(소)의 방문여부를 체크해줍니다.

d 배열에는 오른쪽 집단과 매칭된 노드의 정보가 들어갑니다.

예를 들어 1번 소가 2번 축사에 들어가 있으면 d[2] = 1 이 됩니다.

cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        int a, b;
        cin >> a;
        for (int j = 0; j < a; j++) {
            cin >> b;
            v[i].push_back(b);
        }
    }
    for (int i = 1; i <= n; i++) {
        memset(checked, false, sizeof(checked));
        if (dfs(i))ans++;
    }
    cout << ans;

소의 갯수 n과 축사의 갯수 m을 입력받아 정보를 v벡터에 저장합니다.

10번째 줄을 보면 1번 소부터 시작해서 축사에 매칭을 시킬 것입니다. 매번 매칭을 시도할 때 마다

체크 된 배열을 모두 false로 초기화 해줍니다.

dfs함수가 true를 return하면 i번 노드가 매칭에 성공했다는 의미이므로 ans++ 해줍니다.

bool dfs(int x) {
    if (checked[x])return false;
    checked[x] = true;
    for (auto nxt : v[x]) {
        if (!d[nxt] || dfs(d[nxt])) {
            d[nxt] = x;
            return true;
        }
    }
    return false;
}

dfs를 진행하는 함수입니다.

먼저 왼쪽 부분 노드 1번 소 부터 dfs를 진행하므로 checked[1] =true로 만들어 줍니다.

4번째 줄을 보면 1번 소와 연결된 축사(오른쪽 노드)를 탐색하면서 매칭이 이루어질 수 있는지 확인합니다.

5번째 줄을 보면 d[nxt] = 0 : nxt와 연결된 노드가 없음 

또는 dfs(d[nxt]) = true : nxt와 연결된 노드가 다른 노드와 연결될 수 있음

두가지 조건을 만족하면 true를 return하고 매칭이 성공하게 됩니다. 

---

전체 코드입니다.(maximal flow)

#include<iostream>
#include<algorithm>
#include<climits>
#include<string>
#include<vector>
#include<queue>
#include<stack>
#include<deque>
#include<cmath>
#include<time.h>
#include<cstring>
#include<cmath>
#include<cstring>
#include<limits>
#define inf INT_MAX
using namespace std;
using ll = long long;
using ull = unsigned long long;
int cap[410][410], flow[410][410], cache[410], n, m, ans, source, sink;
vector<int>v[410];
void add_edge(int from, int to, int c);
int Edmond_Karp(int source, int sink);
int main() {
    ios_base::sync_with_stdio(false), cin.tie(NULL), cout.tie(NULL);
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        int a, b;
        cin >> a;
        for (int j = 0; j < a; j++) {
            cin >> b;
            add_edge(i, b + n, 1);
        }
    }
    for (int i = 1; i <= n; i++)add_edge(0, i, 1); //soruce
    for (int i = 1; i <= m; i++)add_edge(i + n, n + m + 1, 1);//sink
    
    cout << Edmond_Karp(0, n + m + 1);
    return 0;
}
void add_edge(int from, int to, int c) {
    v[from].push_back(to);
    v[to].push_back(from);
    cap[from][to] = c;
    //backward edge의 경우 흐르는 유량만큼이 용량이 됩니다.
    //하지만 흐르는 유량이 0이므로 그대로 0입니다.
}
int Edmond_Karp(int source, int sink) {
    int max_flow = 0;
    while (1) { //augmenting path가 없을때까지 반복, bfs로 진행
        queue<int>q;
        q.push(source);
        memset(cache, -1, sizeof(cache));
        cache[source] = 0;
        while (q.size()) {
            int cur = q.front();
            q.pop();
            for (auto nxt : v[cur]) {
                if (cache[nxt] == -1 && cap[cur][nxt] - flow[cur][nxt] > 0) {
                    cache[nxt] = cur;//직전에 어디서 왔는지 저장
                    q.push(nxt);
                    if (nxt == sink)break;
                }
            }
        }
        if (cache[sink] == -1)break; //현재 residual graph에서 sink로 가는 간선이 없음
        int min_cap = 1e9;
        //현재 residual graph 용량의 최솟값을 min_cap에 저장
        for (int i = sink; i != source; i = cache[i]) {
            int bef = cache[i];
            min_cap = min(min_cap, cap[bef][i] - flow[bef][i]);
        }
        max_flow += min_cap;
        //유량을 min_cap 만큼 흘리므로 residual graph를 수정
        for (int i = sink; i != source; i = cache[i]) {
            int bef = cache[i];
            flow[bef][i] += min_cap;
            flow[i][bef] -= min_cap;
        }
    }
    return max_flow;
}

---

전체 코드입니다. (이분 매칭)

#include<iostream>
#include<algorithm>
#include<climits>
#include<string>
#include<vector>
#include<queue>
#include<stack>
#include<deque>
#include<cmath>
#include<time.h>
#include<cstring>
#include<cmath>
#include<cstring>
#include<limits>
#define inf INT_MAX
using namespace std;
using ll = long long;
using ull = unsigned long long;
int n, m,ans;
vector<int>v[410];
bool checked[1010];
int d[1010]; //점유하고 있는 노드의 정보
bool dfs(int x);
int main() {
    ios_base::sync_with_stdio(false), cin.tie(NULL), cout.tie(NULL);
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        int a, b;
        cin >> a;
        for (int j = 0; j < a; j++) {
            cin >> b;
            v[i].push_back(b);
        }
    }
    for (int i = 1; i <= n; i++) {
        memset(checked, false, sizeof(checked));
        if (dfs(i))ans++;
    }
    cout << ans;
    return 0;
}
bool dfs(int x) {
    if (checked[x])return false;
    checked[x] = true;
    for (auto nxt : v[x]) {
        if (!d[nxt] || dfs(d[nxt])) {
            d[nxt] = x;
            return true;
        }
    }
    return false;
}