백준 12895 (화려한 마을) c++

문제

12895번: 화려한 마을

n, m, k가 주어지면 n은 집의 개수, m은 사용할 색의 개수, k는 작업의 개수를 의미합니다.

작업은 C와 Q가 있는데 

C는 C a b c 의 형태로 주어지면 [a, b]구간에 있는 모든 집을 c로 색칠한다는 의미입니다.

Q는 Q a b 의 형태로 주어지면 [a, b] 구간에 있는 모든 집의 색의 가짓수를 출력한다는 의미입니다.

 

작업이 Q a b 일때 [a, b]에 있는 모든 집에 존재하는 색의 가짓수를 출력하는 문제입니다.

 

색의 종류가 30가지 밖에 안된다는 점을 잘 관찰해야 합니다.

lazy segment tree로 30가지 색을 전부 update하면서 서로 다른 색을 체크하는 것은 쉽지 않습니다.

 

lazy segment tree의 장점 중 하나는 update와 쿼리 연산이 동일할 필요가 없다는 것입니다.

예를 들어 update는 합으로 설정할 수 있고, 쿼리는 구간의 max값을 구할 수 도 있습니다.

 

이 문제는 update는 대입연산, 쿼리는 OR 연산으로 실행해주면 됩니다.

30가지 색을 bitmasking하게 되면, 마지막에 OR연산한 쿼리의 켜진 bit수를 세주면 됩니다.

예를들어 1번색은 2^0 만 1이되고 30번색은 2^29에 1이 켜지게 됩니다.

 

update(1, 1, n, 1, n, 1);//모든 집을 1로 초기화
 
void update(ll N, ll s, ll e, ll l, ll r, ll val) {
    update_lazy(N, s, e);
    if (l > e || r < s)return;
    if (l <= s && e <= r) {
        tree[N] = val;
        if (s != e) {
            lazy[N * 2] = val;
            lazy[N * 2 + 1] = val;
        }
        return;
    }
    ll mid = (s + e) / 2;
    update(N * 2, s, mid, l, r, val);
    update(N * 2 + 1, mid + 1, e, l, r, val);
    tree[N] = tree[N * 2] | tree[N * 2 + 1];
}

모든 segment tree를 1번색으로 초기화 해주는 부분입니다.

1번째 줄은 main 함수에서 실행됩니다. 

4번째 줄은 propagate 하는 함수입니다. 

 

전반적으로 code가 이전에 배웠던 구간합 lazy segment tree와 유사합니다. 

다른점은 현재 segment tree에는 누적합이 아니라

구간을 포함하는 집에서 서로 다른 색으로 칠한곳을 count하는 것입니다.

따라서 만약에 1번색으로 칠한곳이 [1, 3] 구간에 포함한 모든 집이라면 

segment tree에서 [1, 3] = 1 이 됩니다. 

7번째 줄을 보면 tree[N]=val 입니다. 단순히 val번 색으로 대입을 해주는 것입니다.

 

17번째 줄을 보면 OR연산을 합니다. 서로 같은 색으로 칠해져있으면 OR연산을 했을 때 

그대로 나올 것입니다. (ex 1 OR 1 = 1 , 2 OR 2 = 2)

반면에 서로 다른 색으로 칠해져 있으면 서로 다른 부분에 bit를 채워줍니다.

(ex 1 OR 2 = 3 => 0001 OR 0010 = 0011) 

 

그러므로 처음에 1로 update를 하게 되면 (ex n=5)

다음 그림처럼 됩니다.

void update_lazy(ll N, ll s, ll e) { //대입연산
    if (!lazy[N])return;
    tree[N] = lazy[N];
    if (s != e) {
        lazy[N * 2] = lazy[N];
        lazy[N * 2 + 1] = lazy[N];
    }
    lazy[N] = 0;
}

Propagate하는 함수입니다.

3번째 줄을 보면

마찬가지로 현재 위치한 tree[N] 에다가 미리 저장해놨던 lazy[N]을 더해주는게 아니라 대입해줍니다.

 

 

cin >> a >> b >> c;
if (a > b)swap(a, b);
d = ((ll)1 << c - 1); //2^c-1
update(1, 1, n, a, b, d); //[a, b]를 d로 초기화

[a, b]에 있는 모든 집을 c로 색칠해주는 부분입니다.

여기서 헷갈린 부분은 1 << c - 1 (shift bit 연산을 먼저 해줄지 -1을 먼저 해줄지 헷갈렸습니다.)

-1을 먼저 하고 진행 합니다. 

즉 1 << 4 - 1 이라면 1 << 3 과 동일합니다.

 

 

ll f(ll N, ll s, ll e, ll l, ll r) {
    update_lazy(N, s, e);
    if (l > e || r < s)return 0;
    if (l <= s && e <= r)return tree[N];
    ll mid = (s + e) / 2;
    return f(N * 2, s, mid, l, r) | f(N * 2 + 1, mid + 1, e, l, r);
}

쿼리 부분입니다. 

구간에 포함된 집의 서로 다른 색깔의 수를 return 해줍니다.

6번째 줄을 보면 return을 할때 더해주는게 아니라 OR연산을 해주어서 서로 다른 색을 Count해주는 것입니다.

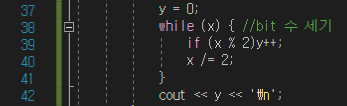
f 함수를 통해 return 값은 x에 저장되있습니다.

y는 x에 bit가 1인수를 세어서 저장해주는 변수입니다.

이제 x는 10진수이기 때문에 2진수 속의 1인 bit를 세주는 작업이 필요합니다.

예를 들어 x가 15이면 15 는 이진수로 1111 입니다. 따라서 총 4가지 색이 서로다른것입니다.

이제 1의 갯수 4를 추출해내기 위해 

2로 나누어떨어지지 않으면 bit 1 이 존재하므로 y를 ++ 해주고 x를 2로 나누어 줍니다.

위와 같은 반복을 통해 y에는 x의 1인 bit수가 저장되고

마지막으로 y를 출력해주면 됩니다.

 

번외로 bit수를 세주는 STL이 존재한다고 합니다.

_builitin_popcount(n) : n의 bit 중 1인 것의 개수를 반환 (시간 복잡도 : O(1))

int y = _builtin_popcount(x);

더욱 편하게 사용 가능합니다.

---

전체 코드입니다.

#include<iostream>
#include<algorithm>
#include<vector>
#include<string>
#include<stack>
#include<queue>
#include<deque>
#include<cmath>
#include<map>
#include<set>
using namespace std;
using ll = long long;
using ull = unsigned long long;
const ll  n_ = 4 * 1e6 + 100;
ll tree[n_], lazy[n_], A[n_];
ll n, m, k,a,b,c,d,x,y;
void update_lazy(ll N, ll s, ll e);
void update(ll N, ll s, ll e, ll l, ll r, ll val);
ll f(ll N, ll s, ll e, ll l, ll r);
int main() {
    ios_base::sync_with_stdio(false), cin.tie(NULL), cout.tie(NULL);
    cin >> n >> m >> k;
    update(1, 1, n, 1, n, 1);//모든 집을 1로 초기화
    for (int i = 0; i < k; i++) {
        char temp;
        cin >> temp;
        if (temp == 'C') {
            cin >> a >> b >> c;
            if (a > b)swap(a, b);
            d = ((ll)1 << c - 1); //2^c-1
            update(1, 1, n, a, b, d); //[a, b]를 d로 초기화
        }
        else {
            cin >> a >> b;
            if (a > b)swap(a, b);
            x = f(1, 1, n, a, b);
            y = 0;
            while (x) { //bit 수 세기
                if (x % 2)y++;
                x /= 2;
            }
            cout << y << '\n';
        }
    }
 
    return 0;
}
void update_lazy(ll N, ll s, ll e) { //대입연산
    if (!lazy[N])return;
    tree[N] = lazy[N];
    if (s != e) {
        lazy[N * 2] = lazy[N];
        lazy[N * 2 + 1] = lazy[N];
    }
    lazy[N] = 0;
}
void update(ll N, ll s, ll e, ll l, ll r, ll val) {
    update_lazy(N, s, e);
    if (l > e || r < s)return;
    if (l <= s && e <= r) {
        tree[N] = val;
        if (s != e) {
            lazy[N * 2] = val;
            lazy[N * 2 + 1] = val;
        }
        return;
    }
    ll mid = (s + e) / 2;
    update(N * 2, s, mid, l, r, val);
    update(N * 2 + 1, mid + 1, e, l, r, val);
    tree[N] = tree[N * 2] | tree[N * 2 + 1];
}
ll f(ll N, ll s, ll e, ll l, ll r) {
    update_lazy(N, s, e);
    if (l > e || r < s)return 0;
    if (l <= s && e <= r)return tree[N];
    ll mid = (s + e) / 2;
    return f(N * 2, s, mid, l, r) | f(N * 2 + 1, mid + 1, e, l, r);
}