Lecture 11 & 12

Combinational Logic Analysis (조합 논리)

Generate an even-parity code

even-parity code는 bit안에 1의 개수가 짝수가 되게하는 bit입니다. 주로 오류 검출용으로 사용합니다.

보통 odd(홀수)는 1이고 even(짝수)는 0입니다.진리식을 보면 even + even = even (0 + 0 = 0)even + odd = odd  (0 + 1 = 1)odd + odd = even (1 + 1 = 0)

 

이러한 진리식은 XOR의 2-input truth table과 동일한 결과를 보여줍니다.

A  B     X

0  0     0

0  1     1

1  0     1

1  1     0

따라서 parity bit를 사용할때는 XOR Logic gate를 사용합니다.

 

even parity code는 XOR Gate의 출력 값에 따라 오류를 검출합니다.

XOR 출력 값이 1이면 bit에서 1의 갯수가 홀수입니다.

반면에 출력값이 0이면 bit에서 0의 갯수가 짝수입니다.

이에 따라 parity bit를 넣을지 말지 생각해주면 됩니다.

 

The Universal Property of NAND and NOR Gates

NAND

NAND 는 NOT, AND, OR, NOR Gate를 조합해서 만들 수 있습니다.

먼저 NOT gate는 NAND gate의 input들을 연결해서 만들 수 있습니다. single input을 2-input으로 만드는 것입니다.

AND gate는 NAND gate만으로 만들 수 있습니다.

OR gate는 NAND gate만으로 만들 수 있습니다.

 

NOR

NOR gate 또한 NOT, AND, OR , NAND gate를 조합해서 만들 수 있습니다.

먼저 NOT gate는 모든 input을 합치고 single input을 2-input으로 바꿔줍니다.

OR gate 또한 NOR gate를 이용하여 만들 수 있습니다.

AND gate 또한 NOR gate를 이용하여 만들 수 있습니다.

---

ex)

 

Combinational Logic Using NAND and NOR Gates

NAND

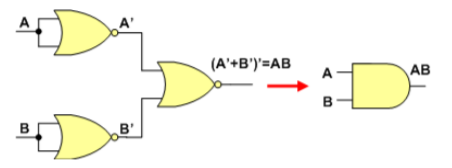
NAND = negative-OR gate 

(AB)' = A' + B'

이러한 Gate를 보면 G2와 G3는 AND Gate의 역할을 하고 G1은 OR Gate의 역할을 하는 것과 같습니다.

따라서 우리는 NAND = negative-OR 인것을 알기 떄문에 G1의 Gate를 NAND가 아닌 negative-OR로 쓸 수 있습니다.

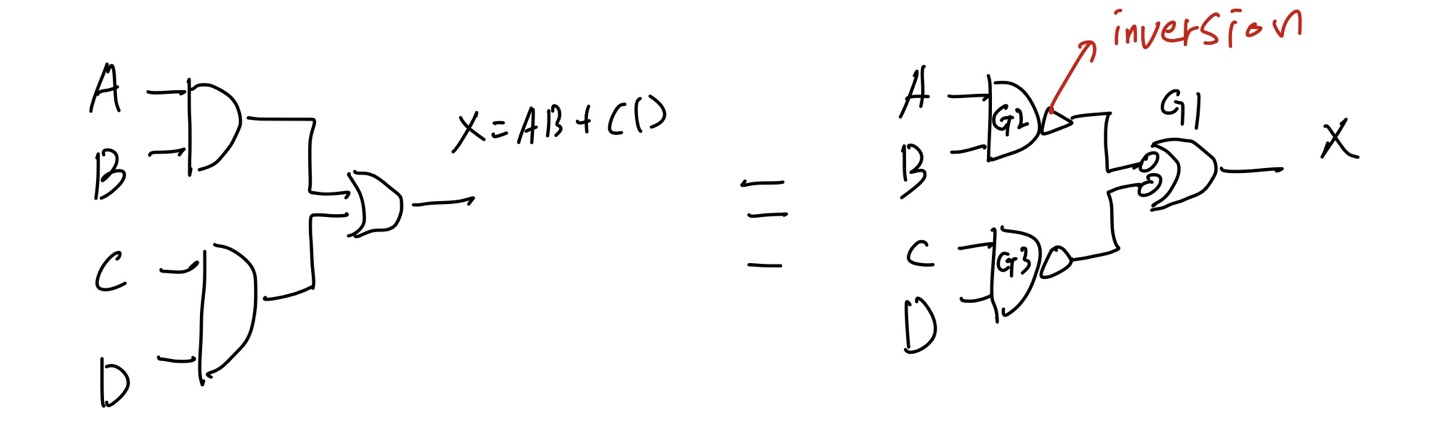
일반적으로 어떤 Gate의 아웃풋이 버블이면 다음 게이트의 입력으로 들어갈때  bubble로 들어갑니다.

다음 두개의 논리회로는 동일한 출력을 가지고 있습니다.

(a)의 논리 회로를 보면 Gate의 출력이 버블이면 다음 Gate의 입력으로 non-bubble로 들어가고 있습니다.

이렇게 최종 출력을 보면 상당히 복잡해 보입니다.

반대로 (b)의 논리 회로는 Gate의 입력과 출력이 non-bubble to non-bubble의 형식을 보여줍니다.

상대적으로 출력이 (a)에 비해 간단합니다.

따라서 우리는 보통 Gate들을 연결할 때 bubble-to-bubble 이나 non-bubble-to-non-bubble을 사용합니다.

 

ex)

Implement each expression with NAND logic using appropriate dual symbols

(a) ABC + DE

(b) ABC + D' + E'

 

NOR

NOR = negative-AND gate

(A+B)' = A'B'

앞에서 본 NAND와 마찬가지로 G3, G2는 OR역할을 하고 G1은 AND 역할을 하고 있습니다.

NOR도 마찬가지로 bubble-to-bubble, non-bobble-to-non-bubble이 적용됩니다.