백준 12865 (평범한 배낭) c++

문제

12865번: 평범한 배낭

유명한 knapsack 알고리즘 문제 입니다.

n개의 물건들이 주어지고 각 물건들은 무게 w와 가치 v가 주어집니다. 가방은 최대 무게 k만큼 짐을 넣을 수 있습니다.

가치를 최대로 하면서 가방에 넣을 수 있는 물건들의 가치의 최댓값을 구하는 문제입니다.

 

dp를 활용해서 문제를 해결하였습니다.

dp[i][j] = i번째 물건을 확인하고 있고 가방의 최대 무게가 j일때 가방에 담긴 물건들의 최대 가치입니다.

 

예를 들어 4개의 물건들이 주어지고 가방의 최대무게는 7이라고 할 때

      w       v

1     6       13  

2     4       8

3     3       6

4     5       12

다음과 같은 정보가 주어지면 

 

 

 

 

 

 

 

 

 

다음과 같은 표를 만들 수 있습니다. 가로줄은 무게를 의미하며 0부터 k(7) 까지 탐색합니다.

세로줄은 주어진 짐의 순번입니다. 

이제 우리는 무게가 0인것 부터 짐의 순번에 따라 확인할 것입니다.

 

1) 무게가 0~2

      w       v

1     6       13  

2     4       8

3     3       6

4     5       12

 

 

 

 

 

무게가 0~2인 짐은 주어진 짐중에 없으므로 0으로 채워집니다.

 

2) 무게가 3

      w       v

1     6       13  

2     4       8

3     3       6

4     5       12

 

 

 

 

 

무게가 3 인짐을 탐색하는 것입니다. 첫번째짐과 두번째 짐은 각각 무게가 6과 4이므로 담을 수 없습니다.

세번째 짐은 3이므로 딱 알맞게 들어갈 수 있습니다.

네번째 짐은 5이므로 들어갈 수 없습니다.

하지만 dp[4][3]의 의미는 4번째 짐까지 탐색하였고 가방의 최대무게가 3일때 최대 가치입니다.

만약 문제가 n이 4이고 k = 3으로 주어졌을때 dp[4][3]이 답이 될것입니다.

따라서 4번째 짐의 무게는 5이기 때문에 수용은 못하지만 이전에 3번째 짐에서 수용을 했기때문에 

최대가치는 6이 되는 것입니다.

 

3) 무게가 4

      w       v

1     6       13  

2     4       8

3     3       6

4     5       12

 

 

 

 

 

 

1번째 짐의 무게는 6이므로 수용불가이고 

2번째 짐의 무게는 4이므로 수용가능합니다.

3번째 짐의 무게는 3이므로 수용가능합니다. 따라서 무게가 3인 가치(6) 과 무게가 4인 가치(8)을 비교하고 

둘중에 더 큰 가치의 값을 넣어주면 됩니다.

4번째 짐의 무게는 5이므로 수용불가 하기 때문에 마찬가지로 이전의 값을 넣어주면 됩니다.

 

4) 무게가 5, 6

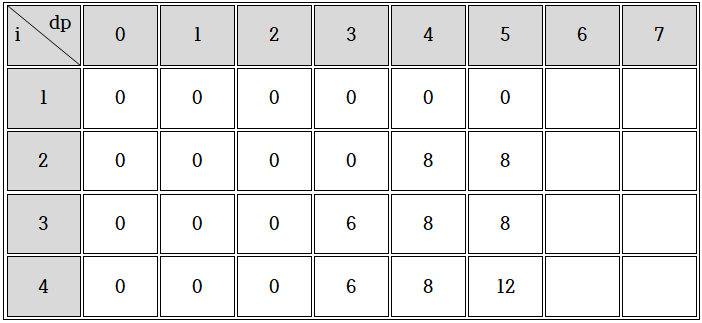
마찬가지로 무게가 5일때 왼쪽 표처럼 삽입하여 주고 무게가 6일때 오른쪽 표처럼 삽입해주면 됩니다.

 

5) 무게가 7일때

      w       v

1     6       13  

2     4       8

3     3       6

4     5       12

 

 

 

 

무게가 7일 경우에는 2가지 방법이 있습니다.

1. 무게가 7인 물건의 가치

2. i번째 무게의 물건의 가치 + 무게가 (7 - i번째 짐의 무게)인 물건의 가치

1과 2 중에 더 큰쪽의 가치가 들어가게 됩니다.

주어진 무게중에서는 7이 없으므로 2번 방법을 해야 합니다.

현재 i = 1이므로 1번째 짐을 탐색하는 과정입니다. 1번째 짐의 무게는 6이므로 가치 13을 포함해서

무게가 1(7 - 6) 인 가치를 더해야 합니다. 무게가 1인 경우 가치가 0이므로 그대로 13이 들거가게 됩니다.

      w       v

1     6       13  

2     4       8

3     3       6

4     5       12

 

 

 

 

 

i = 3인 경우 무게는 3이고 가치는 6입니다. 무게가 4(7 - 3)인 물건의 가치는 8입니다

따라서 6 + 8(14) > 13 이므로 14가 들어가게 됩니다

.최종적으로 표가 만들어 졌습니다.

---

이를 코드로 표현하면 다음과 같습니다.

for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= k; j++) {
            if (j >= weight[i])
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
            else dp[i][j] = dp[i - 1][j];
        }
    }

i와 j 둘다 1부터 탐색합니다.

현재 i번째 무게를 고정하고 가방의 무게가 j~k 까지 변화하면서 i번째 무게를 넣을 수 있는지 없는지 탐색합니다.

3번째 줄을 보면 i번째 무게의 짐(weight[i])이 가방의 무게(j)보다 작으면 즉, i번째 무게의 짐을 가방에 넣을 수 있다면

dp값을 갱신해주면 됩니다. 

4번째 줄을 보면 dp[i - 1][j - weight[i]]의 의미는 i번째 무게의 물건의 가치 + 무게가(가방의 무게 - i번째 짐의 무게)인 물건의 가치를 의미합니다. 

예를 들어 가방의 무게가 7이면 (1, 6) (2, 5) (3, 4)의 조합의 가치 합으로 이해하시면 됩니다.

---

for (int i = 1; i <= n; i++)
        for (int j = k; j - weight[i] >= 0; j--)
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

위의 코드를 좀더 효율적으로 바꾼 코드입니다. 위의 코드는 dp배열을 2차원으로 선언하였기 때문에 

필요없는 무게에 대해서도 중복탐색을 허용하였습니다. 

지금 코드는 2번째 for문이 k부터 시작해서 j-weight[i] >=0 까지 탐색합니다. 

즉, i번째 무게의 짐을 현재 가방의 무게(j)에 넣을 수 있는것들만 탐색한다는 의미입니다.

---

전체 코드입니다.

#include<iostream>
#include<algorithm>
#include<climits>
#include<string>
#include<vector>
#include<queue>
#include<stack>
#include<deque>
#include<cmath>
#include<time.h>
#include<cstring>
#include<cmath>
#include<cstring>
#include<limits>
#define inf INT_MAX
using namespace std;
using ll = long long;
using ull = unsigned long long;
int dp[100001];
int weight[101], value[101];
int main() {
    ios_base::sync_with_stdio(false), cin.tie(NULL), cout.tie(NULL);
    int n, k;
    cin >> n >> k;
    
    for (int i = 1; i <= n; i++) {
        cin >> weight[i] >> value[i];
    }
    
    for (int i = 1; i <= n; i++)
        for (int j = k; j - weight[i] >= 0; j--)
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
 
    cout << dp[k];
 
    return 0;
}