#8 Maximum flow, Bipartite matching

그래프 이론에서 network flow 라는 개념은 매우 중요

여러가지 개념에 대해서 알아보고, maximum flow를 구하는 알고리즘을 알아보자

물을 흐르게 하는 상수도 처럼 생각해 보면 쉬울 수 있다.

 

용량(capacity) : 어떤 간선에 대해 존재하는 개념 flow를 흐르게 할 수 있는 한계.

유량(flow) : 정점 u와 v를 잇는 간선이 있을 때, 그 간선에 존재하는 용량 이하 만큼의 유량을 흘릴 수 있다.

소스(source) : 소스는 정점에 존재하는 개념인데, 소스에서만 유량을 발생시킬 수 있다.

싱크(sink) : 싱크도 정점에 존재하는 개념인데, 소스에서 발생한 유량이 흘러온다.

그래프의 간선들의 용량을 표현한 그림이다.

예를 들어 1 -> 2 의 유량이 6까지만 흐를 수 있다.

소스는 1번정점, 싱크는 7번 정점으로 한다.

소스는 보통 s, 싱크는 t로 표현한다.

 

이제 그래프에 유량을 흘려 줄 텐데, 각각의 정점에서는 소스와 싱크를 제외하고는 들어오는 유량의 양과

나가는 유량의 양이 같아야 한다.

또 각 유량은 간선의 용량 이하로 흘러야 한다.

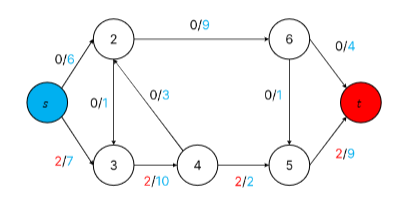
그래프에 현재 간선의 용량과 현재 유량의 양을 함께 표현해보자

왼쪽은 현재의 유량이고 오른쪽은 용량입니다.

이런식으로 표현한 그래프를 flow network라고 합니다.

maximal flow란 설명했던 성질들을 해치지 않으면서 최대로 흘렸을 때의 유량의 양입니다. 

예를 들어 source에다가 유량을 2 정도 흘러주면 위의 그래프와 같습니다.

이제 유량을 5정도 흘리면 위의 그래프와 같습니다.

유량 5가 밑으로 갈 수 없는 이유는 4 -> 5 로 갈 때 이미 유량이 2로 차있기 때문입니다.

따라서 유량 5는 처음에 source로 시작해서 2로 가게 되고 6으로 가게 된후 

6에서 sink로는 4밖에 가지 못하므로 4를 보내주고 나머지 1은 5로 보내주고 5에서 sink로 1을 더 추가해

줍니다.

최종적으로 maximal flow는 7 입니다.

 

이제 maximal flow알고리즘을 알아 보겠습니다.

residual graph : flow network 에서 간선을 forward edge, backward edge 2개로 쪼갠다.

      -forward edge : 용량은 capacity - flow로 , 원래 간선과 같은 방향이다.

      -backward edge : 용량은 flow로 , 원래 간선과 반대 방향이다.

augmenting path : residual graph 에서 source에서 sink까지의 simple path.

forward edge

forward edge 부터 선을 표시해주면 위의 그래프와 같습니다.

forward edge의 용량은 capacity - flow입니다. 즉, 유량을 보낼 수 있는 용량을 표시하는 것입니다.

용량 0은 표시할 필요 없습니다.

residual graph

backward edge는 지금 얼마만큼 흐르고 있느냐, 얼마만큼 뒤로 돌려보낼 수 있느냐를 표현합니다.

backward edge의 용량은 flow입니다.

 

maximal flow가 맞다면 residual graph에서 augmenting path가 존재하지않는다

따라서 우리는 residual graph에서 augmenting path가 존재한다면 maximal flow가 아님을 알 수 있다.

존재하는 경우 augmenting paht에서 경로들 중 최소 capacity만큼의 flow를 흘리는 것을 반복해서 maximum flow를

찾아 줄 것이다. 

위의 그래프의 경우 source에서 sink(t)로 가는 경우(augmenting path) 가 없기 때문에 maximal flow입니다.

 

이제 직접 구해보겠습니다.

먼저 residual graph를 그려줘야 하기 때문에 처음에 forward edge부터 그려줍니다.

back ward edge

먼저 s -> t로가는 augmenting path를 검사합니다.

두껍게 표시한 선이 augmenting path이므로 존재합니다.

따라서 아직 max flow가 아니고, 이 경로의 용량 최솟값 2만큼 유량을 흘러 줍니다.

다음에 backward edge를 그려줍니다. 

또 이제 augmenting path를 검사해줍니다.

두껍게 표시한 선이 augmenting path이므로 존재합니다.

따라서 아직 max flow가 아니고, 이 경로의 용량 최솟값 4만큼 흘려 줍니다.

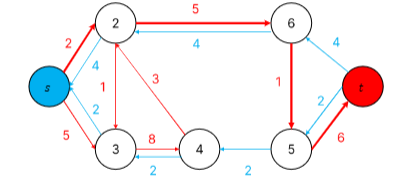
또 위의 그래프 처럼 residual graph가 바뀝니다.

또 이제 augmenting path를 검사해줍니다.

두껍게 표시한 선이 augmenting paht이므로 존재합니다.

따라서 아직 max flow가 아니고, 이 경로의 용량 최솟값 1만큼 흘려줍니다.

또 위의 그래프 처럼 residual graph가 바뀝니다.

이제는 augmenting path가 존재하지않으므로 

지금 까지 흘려준 유량의 누적합이 7이므로 maximum flow는 7이 됩니다.

 

backward edge의 역할을 결국 이전에 흘러 보냈던 유량을 알려주는 기능을 하는 동시에 

흘려주어야 하는 유량의 최솟값이 아닌 경우에 다시 되돌아 와야 하는데 이는 backward edge에 저장되있어

취소 하기에도 용이하다.

예를 들어 위의 그래프를 보면 6 -> 5로 가는 유량은 1이다. 1을 흘려 보낸후

5 -> 6 으로 가는 backward edge 에는 1이 기록되었다. 

 

residual graph에서 augmenting path를 찾는 방식이 dfs냐 bfs냐에 따라서 시간복잡도가 달라진다.

dfs로 augmenting path를 찾게 되면, 시간복잡도는 O(FE)이고 Ford-Fullkerson Algorithm이라고 한다.(F=용량의최댓값)

bfs로 augmenting path를 찾게 되면, 시간복잡도는 min(O(FE), O(VE^2) 이고 Edmonds-Karp Algorithm이라고 한다.

보통 bfs로 구현해주는게 효율적이다.

 

Maximum flow는 여러가지 문제상황에 있어서 아주 효과적인 해결방법이다.

실생활에서도 효과적으로 사용할 수 있다. (ex 동아리 면접 시간 정하기)

 

이분매칭

matching : 공통 정점을 가지지 않는 간선의 집합

이분 그래프에서 매칭은 , flow로 치환 될 수 있기 때문에 다항시간내에 풀 수 있다.

이분 매칭의 성질을 이용하면 flow없이 O(VE)에 문제를 풀 수 있다. 

구현이 훨씬 간단하기 때문에 많이 사용된다.

 

왼쪽 정점 그룹을 훑으면서 아직 매칭이 안 된 애들이 있으면서 간선을 흝으면서 매칭을 늘릴 수 있는지를

살펴본다.

그리고 늘릴 수 있다면 매칭을 해준다.

예를 들어 1번 2번 3번 친구가 1번 방, 2번 방 3번 방에 갈 수 있다

1번 친구는 1, 2, 3번 방에 가고 싶어하고

2번 친구는 1번 방에 가고 싶어하고

3번 친구는 2번 방에 가고 싶다.

1번 친구는 1번 집이 아무도 매칭이 안되어서 1번집과 매칭합니다 ans = 1

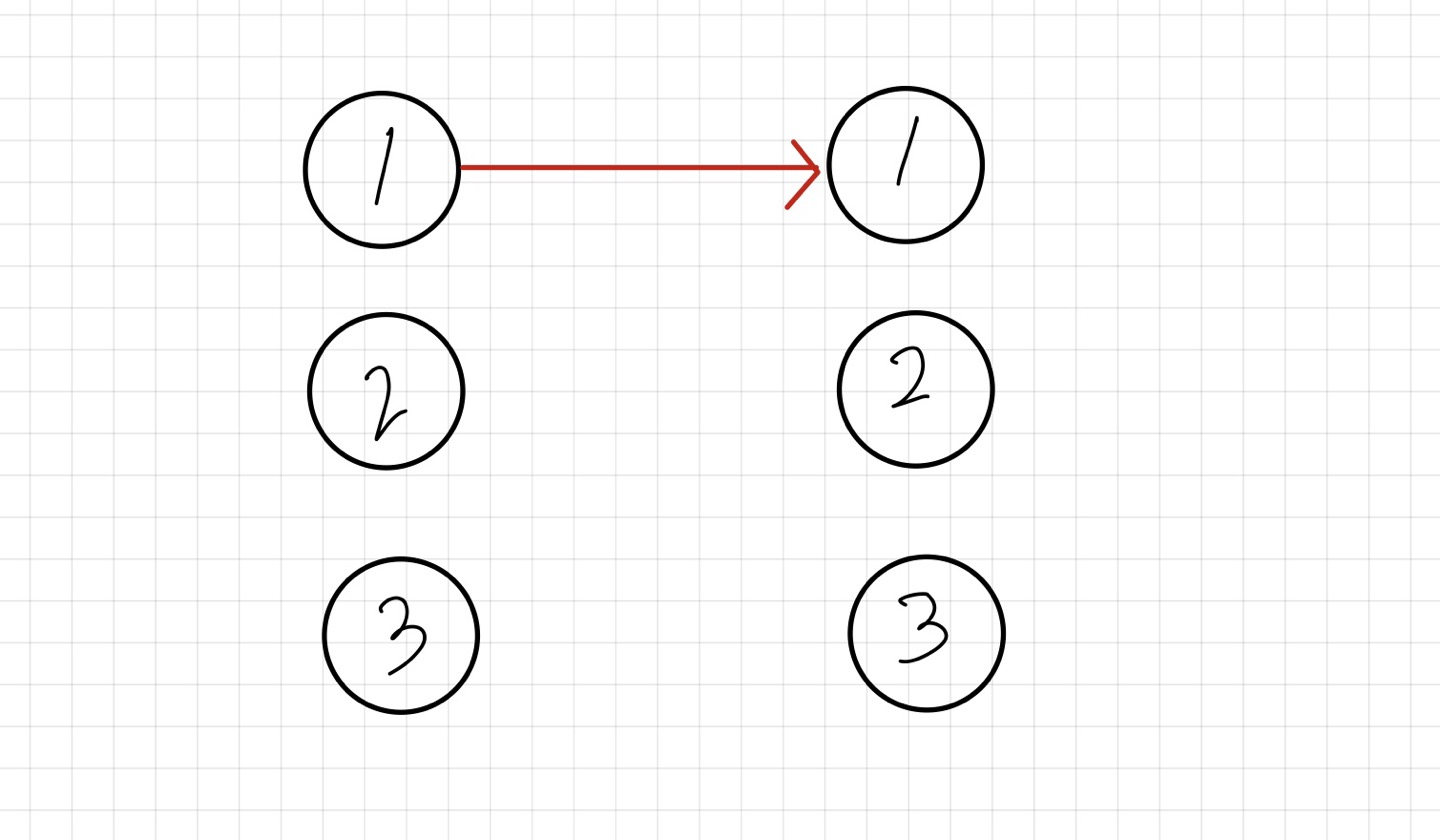
2번 친구는 1번 집에 가고 싶습니다. 하지만 1번 집은 1번 친구와 매칭이 되있기 때문에 1번친구 에게

다른 집으로 갈 수 있는지 물어보고 1번 친구는 2번 집으로 갈 수 있어서 1번 친구는 2번 집에 가고

2번 친구는 1번 집에 매칭이 되었습니다. ans = 2

3번 친구는 2번 집에 가고 싶습니다. 하지만 2번 집은 1번 친구와 매칭이 되있기 때문에 1번 친구에게 

다른 집으로 갈 수 있는지 물어보고 1번 친구는 3번 집으로 갈 수 있어서 1번 친구는 3번 집에 가고

3번 친구는 2번 집에 매칭이 되었습니다. ans = 3

위와 같은 알고리즘으로 진행되는것이 이분 매칭입니다.

예시문제

백준 2188 (축사 배정) c++