# 8 Graph & Tree

Graph?

이산수학에서 사용

특정 집합의 추상화된 원소들에 대하여, 원소들의 일부분이 어떤한 관계로 "연결되어있음"을 나타내는

수학적 구조의 일종

연결 관계가 있는 집합을 나타내는 데에 좋은 자료구조이다.

정점 v의 차수(degree) deg(v)

정점 v와 연결되어있는 정점의 수

ex) deg(1) = 2

 

경로(path) p

정점의 나열로써, 인접한 정점 사이에 간선이 있는 경우

p = {1, 3, 4, 5, 3}

 

단순 경로 (simple path) p

경로로써, 중복되는 정점이 없는 경우

p = {1, 3, 4, 5}

 

순환 (cycle) c

경로로써, 시작점과 끝점이 동일한 경우

c = {1, 3, 4, 5, 3, 1}

 

단순순환 (simple cycle) c

순환으로써, 시작점과 끝점을 제외한 중복되는 정점이 없는 경우

c = {3, 4, 5, 3}

 

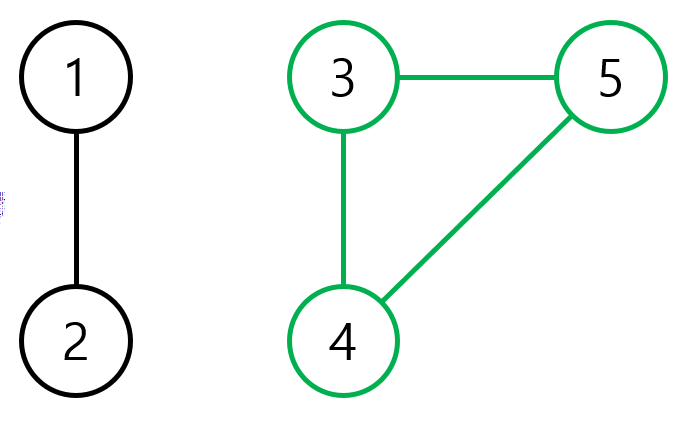
연결 요소 (connected component) C

임의의 두 정점 사이에 경로가 존재하는 부분 그래프

C = {3, 4, 5}

방향 그래프 (시작과 끝이 정해져 있다)

가중치 그래프

 

Graph 구현

int num_edge = 5;
int E[MAXE][2] = {{1, 2}
                  {1, 3}
                  {3, 4}
                  {3, 5}
                  {4, 5}};

여기서 u번과 v번의 간선을 추가하고 싶다면 (시간 복잡도 : O(1))

void add_adge(int v, int u){
    E[num_edge++][0] = u;
    E[num_edge][1] = v;
}

여기서 u번과 v번 사이에 간선이 있는지 없는지 확인해보고 싶을 때 시간복잡도 : O(|E|)

bool is_edge(int u, int v){
    for(int i=0; i < num_edge; i++){
        if(E[i][0] == u && E[i][1] == v) return true; 
        if(E[i][0] == v && E[i][1] == u) return true; 
    }
    return false;
}

 

더 효율적인 방법은 없을까?

 

인접행렬

int adj_mat[6][6] =
    {{0, 0, 0, 0, 0, 0},
     {0, 0, 1, 1, 0, 0},
     {0, 1, 0, 0, 0 ,0},
     {0, 1, 0, 0, 1, 1},
     {0, 0, 0, 1, 0, 1},
     {0, 0, 0, 1, 1, 0}};

여기서 u번과 v번의 간선을 추가 하고 싶으면 (시간복잡도 : O(1))

void add_edge(int u, int v){
    adj_mat[u][v] = 1;
    adj_mat[v][u] = 1;
}

여기서 u번과 v번 사이에 간선이 존재하는지 안하는지 알고 싶으면 (시간 복잡도 : O(1))

bool is_edge(int u, int v){
    if(adj_mat[u][v] == 1) return true;
    else return false;
}

공간복잡도 : O(|V|^2)

 

인접 리스트

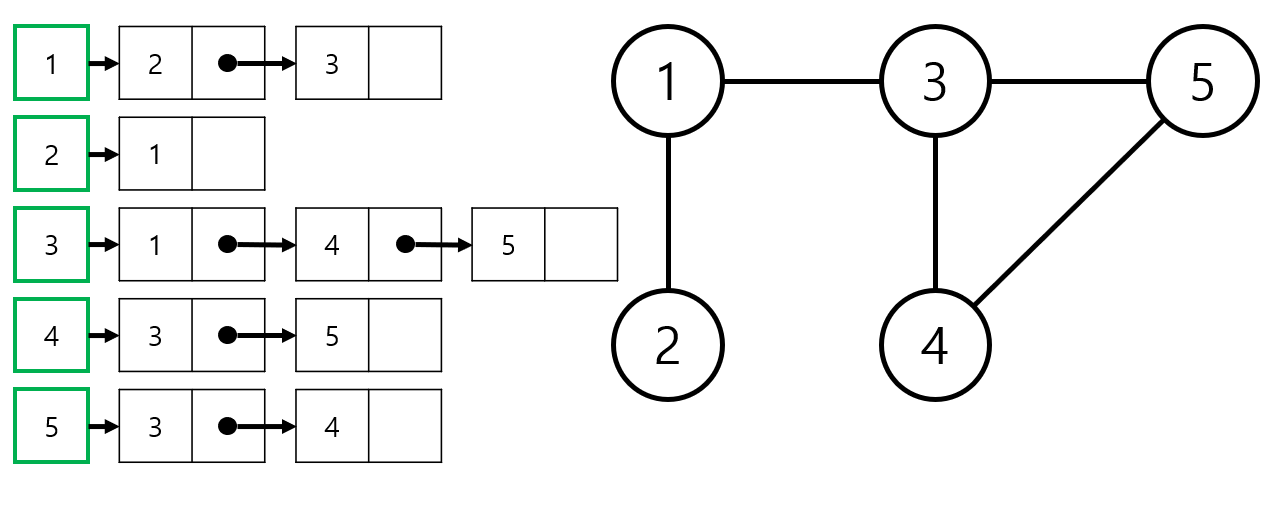
vector<int>adj_list[6] =
    {{}, //adj_list[0]
     {2, 3}, //adj_list[1]
     {1}, //adj_list[2]
     {1, 4, 5}, //adj_list[3]
     {3, 5}, //adj_list[4]
     {3, 4}}; //adj_list[5]

여기서 u와 v에 간선을 추가 하고 싶다면 (시간복잡도 : O(1))

void add_edge(int u, int v){
    adj_list[u].push_back(v);
    adj_list[v].push_back(u);
}

여기서 u와 v에 간선이 있는지 없는지 알고싶다면 (시간복잡도 : O(deg(v))

bool is_edge(int u, int v){
    for(int e : adj_list[u]) if(e == v) return true;
    return false;
}

 

공간복잡도 : O(|E|)

---

Tree?

연결 그래프이면서 순환(cycle)을 갖지 않는 그래프 (V >=3)

 

TFAE (다 동치)

1) 그래프 T가 트리이다.

2) T는 연결 그래프이면서 순환을 갖지 않는다.

3) T는 연결 그래프이면서 |V| = |E| + 1을 만족한다.

4) T의 임의의 서로 다른 두 정점 사이의 경로가 정확히 하나 존재한다.

 

트리 T의 높이(height) h(T)

루트 정점으로부터 가장 멀리 있는 정점까지의 거리

h(T) = 2

 

K-진 트리 

모든 정점이 K개 이하의 자식 정점을 갖는 트리

 

이진 트리 (binary tree)

 

포화 이진 트리(prefect binary tree)

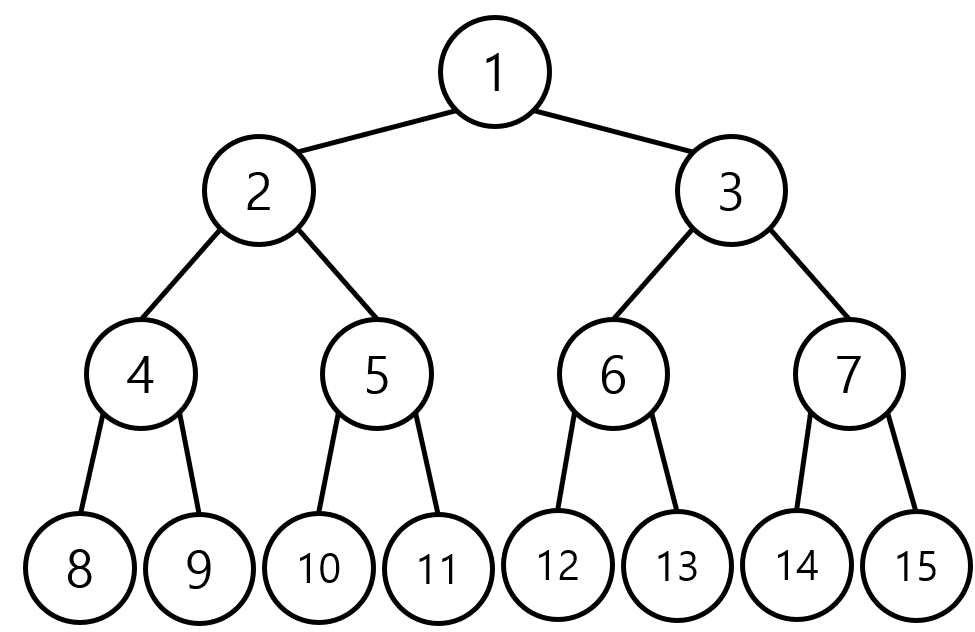
리프 정점을 제외한 모든 정점이 2개의 자식 정점을 가지며, 모든 리프 정점의 깊이가 동일한 트리

높이가 h라면 정점의 개수는 2^h+1 - 1개 이다.

 

완전 이진 트리(complete binary tree)

포화 이진 트리에서 오른쪽의 리프 정점들의 일부 제거된 트리

 

이진 트리의 순회 (tree traverse)

1) 전위 순회 (preorder traverse)

1) 루트 정점을 방문한다.

2) 왼쪽 부트리를 전위 순회한다.

3) 오른쪽 부트리를 전위 순회 한다.

 

2) 중위 순회 (inorder traverse)

1) 왼쪽 부트리를 중위 순회 한다.

2) 루트 정점을 방문한다.

3) 오른쪽 부트리를 중위 순회 한다.

 

 

 

 

 

 

 

 

 

 

3) 후위 순회 (postorder traverse)​

1) 왼쪽 부트리를 후위 순회 한다.

2) 오른쪽 부트리를 후위 순회한다.

3) 루트 정점을 방문한다.