#10 Disjoint Set & Minimum Spanning Tree

1) 정점 v가 속해 있는 그룹은 몇 번 그룹인가? (Find)

2) 정점 u가 속한 그룹과 정점 v가 속한 그룹을 합치면 어떻게 되는가? (Union)

정점 인덱스가 속한 그룹의 정보를 다음과 같은 배열에 저장할 수 있습니다.

 

만약 0번 그룹과 5번 그룹을 합치고 싶으면 어떻게 해야 할까?

다음과 같이 배열을 수정할 수 있습니다.

 

시간복잡도

Find : O(1)

Union : O(N) 모든 정점을 순회하면서 바꿔야하기 때문

 

위의 그래프를 조직도 처럼 만들어 보자!

최고 리더는 -1로 해주고 각 노드마다 직속 상사를 배열로 저장하면

다음과 같은 배열이 됩니다.

 

여기서 0번 그룹이 5번그룹과 합치려면 어떻게 해야될까?

다음과 같이 합치면 됩니다.

 

시간 복잡도

Find : O(정점 v가 속한 트리의 높이)

Union : 각 그룹의 대표자를 아는 경우 O(1)

 

우리가 처음에 배웠던 그래프 버전의 시간복잡도는 이미 시간복잡도가 결정되있기 때문에 더 효율적으로

설계를 못합니다.

하지만 아까 그래프를 조직도의 형태인 트리로 관리하면 조건에 따라 시간복잡도가 달라지기 때문에

개선의 여지가 남아있습니다.

 

트리로 관리했을 때 Find의 시간복잡도는 트리의 높이의 따라 결정됩니다.

그러면 트리의 높이를 N보다 작게 해서 효율적이게 할 수 없을까?

 

Disjoint-set(서로소 집합), Union-find 자료구조

원소가 겹치지 않는 집합들에 대해, 집합의 대표 원소 탐색, 집합의 병합 등을 효율적으로 할 수 있는 자료 구조 

 

1) 같은 집합에 속하는 원소들의 트리의 형태로 나타낸다.

2) 각 트리의 루트 정점이 그 트리의 해당하는 집합의 대표 원소가 된다. 

3) 트리의 높이를 효율적으로 관리한다.

 

Union 연산 (트리의 높이를 최소로 만들기)

왼쪽의 트리를 합치려 할때 가운데 버전과 오른쪽 버전이 있습니다.

우리는 트리의 높이가 최소로하기를 원하므로 가운데 버전이 더 좋습니다.

 

따라서 우리는 결론을 내릴 수 있습니다.

트리의 높이가 큰쪽으로 붙으면 됩니다.

그렇게 되면 합쳐진 최종 트리의 높이는 높이가 큰쪽의 트리입니다.

만약 트리의 높이가 서로 같다면 그냥 두 트리중 아무곳이나 가서 붙으면 됩니다.

그렇게 되면 최종 합쳐진 트리는 트리의 높이 +1 입니다.

 

그러면 위의 규칙대로 트리의 높이를 최대로 할려면 어떻게 해야 할까?

 1 ~ 4 번 노드가 서로 높이가 똑같을 때

1번 노드의 0번 노드가 붙고 

2번 노드와 3번 노드가 붙고

마지막으로 1번 노드에 2번 노드가 붙으면 

위의 규칙을 만족하면서 트리의 최대한의 높이를 만들 수 있습니다.

즉 4개의 노드로 최대의 높이를 만들면 2가 됩니다.

높이 = 2

 

 

마친가지로 1 ~ 8 개의 높이가 같은 노드를

합쳐서 높이가 최대로 만들면

왼쪽의 그림과 같아집니다.

즉, 8개의 노드로 최대의 높이를 만들면 3이 됩니다.

 

 

 

 

 

 

 

위의 그림을 규칙을 찾으면

트리의 높이가 h만큼 높아지기 위해서는 적어도 2^h 개의 정점이 필요합니다.

따라서 2^h 개의 정점을 가진 트리의 높이는 h를 넘지 않습니다.

n개의 정점을 가진 트리의 높이는 O(log N)을 넘지 않습니다.

 

구현

트리의 높이를 서로 비교하고 높이가 더 높은 트리에 붙어야 합니다. 따라서 각 트리의 높이의 정보를 저장하는

높이 배열이 필요합니다.

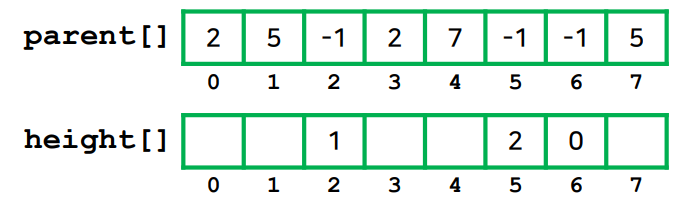
높이 배열은 트리의 루트 노드가 대장이므로 대장 노드의 인덱스에만 정보가 들어가면 됩니다.

 

Find 함수 (u정점이 속한 그룹의 대표 번호를 return)

int Find(int u) {
	if (parent[u] == -1)return u;
	return Find(parent[u]);
}

시간 복잡도 : O(log N)

공간 복잡도 : O(N)

 

좀더 효율적으로 아래와 같이 수정 할 수 있습니다. (Path Compression 경로 압축)

int Find(int u) {
	if (parent[u] == -1)return u;
	return parent[u] = Find(parent[u]);
}

시간 복잡도 , 공간복잡도 : 

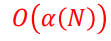
에커만 함수의 역함수 (자세히 모름..) 대충 O(1) 입니다.

 

Union 함수 (정점 u와 정점 v가 속한 그룹의 트리를 합칠 수 있는지 확인)

bool Union(int u, int v) {
	u = Find(u); v = Find(v);
	if (u == v)return false; //서로 대장이 같으면 합치지 못함

	if (height[u] < height[v])swap(u, v);
	parent[v] = u;

	if (height[u] == height[v])height[u]++;
	return true;
}

시간 복잡도 : O(log N)

공간 복잡도 : O(N)

---

MST (최소 신장 트리)

신장 트리 (spanning tree) T

그래프의 모든 정점을 포함하는 트리

 

최소 신장 트리 (minimum spanning tree) T

신장 트리 중 트리를 구성하는 간선의 가중치 합이 가장 작은 신장 트리

가중치가 가장 작은 간선 e는 MST에 포함된다.

남아있는 간선 중 가장 작은 간선 t가 순환을 이루지 않는 다면, t는 MST에 속한다.

 

Kruskea's Algrithm (크루스칼 알고리즘)

1) 주어진 그래프의 간선 집합 E를 가중치에 따라 정렬 (O(|E|log|E|) = O(|E|log|V|))

2) 가중치가 가장 작은 간선부터 순서대로 다음과 같이 처리한다. O(t cycle) = O(|V| + |E|)

    2-1) 이미 MST에 포함된 간선과 순환을 이룰 경우, 무시한다.

    2-2) 그렇지 않은 경우 MST에 포함시킨다.

3) 모든 간선을 다 처리하거나 MST에 |V| - 1 개의 간선이 포함될 때까지 2)를 반복한다. (O(|E|(|V| + |E|))

(일반적으로 순환의 유무를 검사할때는 DFS를 활용한다)

시간 복잡도 : O(|E|log |V|) + O(|V| + |E|) + O(|E|(|V| + |E|)) = O(|E^2|)

 

시간 복잡도가 오래걸리기 때문에 좀더 효율적으로 바꿔보자

 

간선의 양 끝점 u와 v가 같은 트리(집합)에 존재 = 순환이 생긴다.

간선의 양 끝점 u와 v가 다른 트리(집합)에 존재 = 순환이 생기지 않는다.

따라서 Disjoint set 자료구조를 이용해 순환이 있는지 여부를 빠르게 판별할 수 있다.

 

구현

1) 주어진 그래프의 간선 집합 E를 가중치에 따라 정렬 

struct edge {
	int u, v;
	int c;
	bool operator<(edge rhs) {
		return c < rhs.c;
	 }
};
vector<edge>Edge;
int V, E;
scanf("%d%d", &V, &E);

for (int i = 0; u, v, c; i < E; i++) {
	scanf("%d%d%d", &u, &v, &c);
	Edge.push_back({ u, v, c });
}
sort(Edge.begin(), Edge.end());

2) 가중치가 가장 작은 간선부터 순서대로 다음과 같이 처리한다. 

    2-1) 양 끝점 u, v가 같은 그룹에 속할 경우, 무시한다.

    2-2) 그렇지 않은 경우 MST에 포함시키고 u, v가 포함된 그룹을 병합한다.

int ans = 0;
for (auto e : Edge) {
	int u = e.u, v = e.v, c = e.c;

	if (Union(u, v)) {
		ans += c;
	}
}

3) 모든 간선을 다 처리하거나 MST에 |V| - 1 개의 간선이 포함될 때까지 2)를 반복한다. 

 

예시문제

백준 1939 (중량제한) c++