백준 9251, 9252 (LCS 1, 2) C++

문제

9251번: LCS

LCS란 최장공통 부분 수열이라는 의미로 예를 들어

ACAYKP

CAPCAK

두개의 문자열이 주어지면 공통 부분 수열들이 존재합니다.

A

AC

ACA

ACAK

여기서 제일 길이가 긴 ACAK가 LCS가 됩니다.

 

LCS의 길이를 구하는 방법은 여러가지가 있습니다.

그 중 2차원 배열을 사용해 DP 형식으로 풀어보겠습니다.

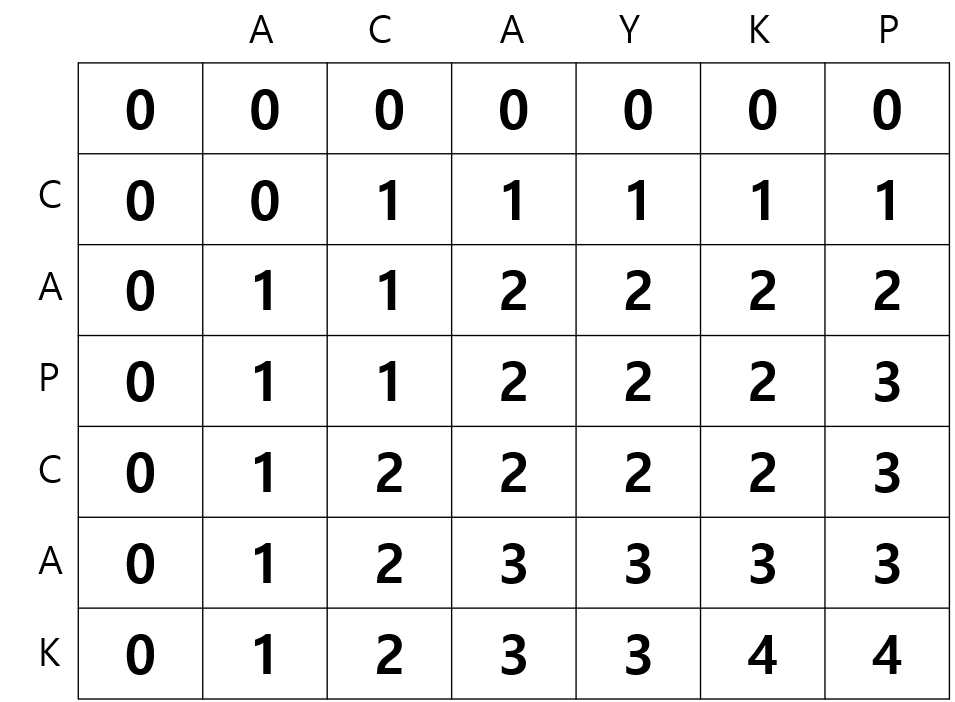
먼저 dp의 인덱스가 0인 부분을 모두 0으로 넣어줍니다.

dp[1][1]부터 시작합니다.

 

점화식은 다음과 같습니다.

st1 = "ACAYKP"

st2 = "CAPCAK"

int a = st1.length();
int b = st2.length();

for (int i = 1; i <= a; i++) {
	for (int j = 1; j <= b; j++) {
		if (st1[i - 1] == st2[j - 1])
			dp[i][j] = dp[i - 1][j - 1] + 1;
		else
			dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);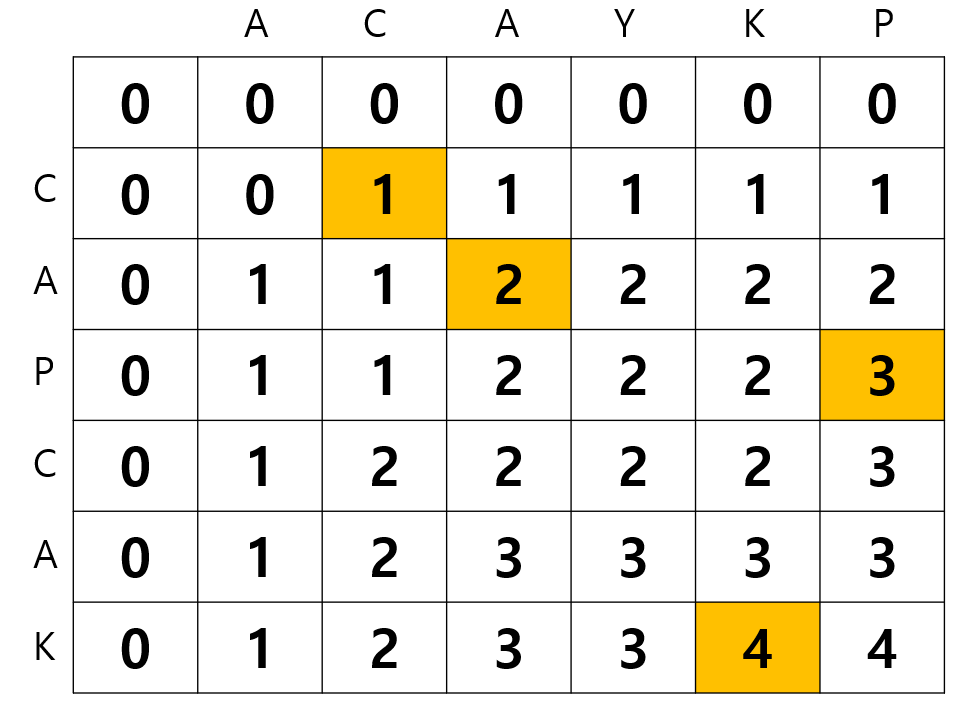
	}
}

dp의 값이 변화하는 구간이 노란색으로 칠해져 있습니다.

이는 일치하는 부분수열을 발견한 구간입니다.

일치한 부분을 발견했으면 dp[i][j] = dp[i-1][j-1] + 1 입니다.

일치한 부분을 발견하지 못했으면 dp[i][j] = max(dp[i-1][j], dp[i][j-1]) 입니다. 즉, 뒤와 위에 있는 것중 큰 값을

넣어주면 됩니다.

 

정답은 마지막에 dp배열의 마지막 인덱스를 출력해주면 LCS의 길이가 나옵니다.

 

문제

9252번: LCS 2

이번 문제는 위와 같이 LCS의 길이를 구하고 직접 LCS까지 구하는 문제입니다.

위의 DP표를 자세히 보면 LCS를 구할 수 있습니다.

우리는 DP값이 1씩 늘어나는 부분만 체크해주면 구할 수 있습니다.

DP 배열의 마지막 부분 부터 시작해서 탐색을 진행할 수 있습니다.

점화식을 세워보면

DP의 뒤쪽, 위쪽 중 값이 같은 곳으로 이동합니다.

만약 DP의 뒤쪽, 위쪽 둘다 값이 다르면 DP의 값이 변경한 것이므로 대각선으로 이동합니다.

int a = st1.length();
int b = st2.length();
vector<char>ch;

while (dp[a][b] != 0) {
	if (dp[a][b] == dp[a][b - 1]) //뒤쪽
		b--;
	else if (dp[a][b] == dp[a - 1][b]) //위쪽
		a--;
	else if (dp[a][b] - 1 == dp[a - 1][b - 1]) { //대각선
		ch.push_back(st1[a-1]);
		a--;
		b--;
	}
}
reverse(ch.begin(), ch.end());

---

전체 코드입니다. (9252번 기준)

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <cmath>
#include <map>
#include <set>
#include <tuple>
#define MAX 2100000000
#define inf LONG_MAX
#define big(a, b) a > b ? a : b
using namespace std;
using ll = long long;
using ull = unsigned long long;
string st1, st2;
int dp[1001][1001];
vector<char>ch;
int main() {
    ios_base::sync_with_stdio(false), cin.tie(NULL), cout.tie(NULL);
    cin >> st1 >> st2;
 
    int a = st1.length();
    int b = st2.length();
 
    for (int i = 1; i <= a; i++) {
        for (int j = 1; j <= b; j++) {
            if (st1[i - 1] == st2[j - 1])
                dp[i][j] = dp[i - 1][j - 1] + 1;
            else
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
        }
    }
    cout << dp[a][b]<<'\n';
 
    while (dp[a][b] != 0) {
        if (dp[a][b] == dp[a][b - 1])
            b--;
        else if (dp[a][b] == dp[a - 1][b])
            a--;
        else if (dp[a][b] - 1 == dp[a - 1][b - 1]) {
            ch.push_back(st1[a-1]);
            a--;
            b--;
        }
    }
    reverse(ch.begin(), ch.end());
 
 
 
    for (auto nxt : ch)cout << nxt;
 
 
    return 0;
}