-
Chapter 15 (Greedy Algorithms)알고리즘 설계와 분석 2022. 12. 11. 00:09728x90
An Activity-Selection Problem

activity들의 시작 시간은 s이고 끝나는 시간은 f이다.
여기서 최대 몇개의 activity들을 할 수 있을지 구하는 것이다.
예를 들어 3번째 activity는 0분에 시작해 6분에 끝난다.
{3, 9, 11}을 선택하면 {0~6}, {8~11}, {12~16}의 시간들을 즐길 수 있다.
즉, 시간이 겹치지 않으면서 최대로 많은 activity를 하는 것이 목표이다.
그리디 알고리즘을 활용해 최적의 결과만을 선택하면 결국 최적의 결과를 얻을 수 있다.
최적의 경우는 구할 수 있지만, 모든 최적의 경우는 다 구할 수 없다.
그렇다면 그리디 선택을 어떻게 할것인가?
현재 시간을 기준으로 할 수 있는 끝나는 시간이 가장 빠른 활동만을 계속하는 것이다.
예를 들어 1번 activity를 보면 가장 먼저 끝나는 시간이고(4) 그 다음에는 4분 이후에 시작하는 결과들 중
가장 빨리 끝나는 활동(activity 4)하는 방식이다. 이런식으로 선택하는 것이 최적의 해이다.

재귀 함수 버전 위 의사 코드는 이미 {s, f}가 오름차순으로 정렬했다고 가정하고 시간 복잡도가 O(N)을 보장한다.
만약 정렬되지 않을 경우 정렬까지 포함하면 시간 복잡도가 O(log n)이 된다.


iterative 버전 시간복잡도는 recursive 버전과 똑같다.
The Knapsack Problems

배낭 1개에 담을 수 있는 무게에 최댓값이 정해져 있고, 일정 가치(VALUE)와 무게 (WEIGHT)가 있는
짐(ITEM)을 배낭에 넣을 때, 가치(VALUE)의 합이 최대가 되도록 짐을 고르는 방법을 찾는 문제이다.
1) 짐 (ITEM)을 쪼갤 수 있는 경우의 배낭 문제를 분할 가능 배낭문제(Fractional Knapsack Problem)
=> greedy 알고리즘 사용
2) 짐 (ITEM)을 쪼갤 수 없는 경우의 배낭 문제를 0-1 Knapsack problem
=> dp 사용
배낭에 물건을 넣을 때 , 우리가 선택할 수 있는 방법은 두가지가 있다.
1. 물건을 넣는다.
2. 물건을 넣지 않는다.
만약 현재 내가 넣으려고 하는 물건의 무게가 전체 제한 무게를 초과한다면, 선택지는 물건을 넣지 않는 것 밖에
없다. 따라서 다음과 같은 식이 만들어진다.

P는 최대가치를 의미한다.
i는 현재 넣은 물건의 번호, w는 배낭에 넣을 수 있는 최대 무게를 의미한다.
w_i 는 i번째 물건에 대한 무게를 의미한다.
1) 당연히 i = 0 또는 w = 0이면 최대 가치는 0이다.
2) i번째 물건이 최대 무게를 초과한다면 i번째 최대가치를 바로 i-1번째 물건을 넣을 경우의 가치로 정한다.
3) 만약 더 넣을 수 있다면 선택지는 다시 두가지로 나뉜다.
1. 새로운 물건을 넣지 않는다.
2. 새로운 물건을 넣기 위해 현재 물건을 넣을 공간을 만들어서 물건을 넣는다.
(현재 물건을 넣기 위해 넣었던 물건을 뺐을 때의 가치에 현재 물건의 가치를 더해주면 된다.)
우리는 최대 가치를 원하기 때문에 두 경우 중 더 큰값을 선택하게 될 것이다.

w[i]는 i번째 물건의 무게를 의미한다.


Huffman Codes
허프만 코드는 데이터를 압축하는 알고리즘이다.
예를 들어 압축하고자 하는 문자열이 ABBCCCDDDDEEEEEFFFFFF 라고 하면
두가지 압축 방법이 존재한다.
1) Fixed-length codes
A ~ F 6개의 문자를 구분하기 위해 3bit가 필요하다 (6 < 2^3)
A = 000, B = 001, C = 010, D = 011, E = 100, F = 101
2) Variable lengths codes
허프만 코드에 의해 나온 값이다.
A = 1000, B = 1001, C = 101, D = 00, E = 01, F = 11
즉, 문자 빈도수가 높은면 짧은 bit로 표현하고, 빈도수가 낮으면 긴 bit로 표현한다.
variable length가 더 짧은 것을 볼 수 있다.
variable length를 사용할때, 압축된 파일을 다시 원상복구하기 위해 prefix-free code를 사용해야한다.
prefix free code는 어떤 이진 코드의 집합이 서로 접두어가 되지않은 코드를 말한다.
예를 들어 {0, 1, 01, 010} 이라는 이진 코드 집합이 있을 떄, 0과 01은 010의 접두어가 될 수 있고,
01은 010의 접두어가 될 수 있기 때문에, prefix free code가 될 수 없다.
만약 이진 코드 집합이 {00. 010. 100, 101} 이라면, 모든 코드가 서로 다른 코드에 대해 접두어가 될 수 없기
떄문에 prefix free code의 조건을 만족한다.
ex) a = 0, b = 1, c = 01이라고 하면
abc라는 string을 0101이라고 압축한다면
나중에 압축을 풀때 0101이 cc라고 풀릴 수도 있고, abab라고 풀릴 수도 있다.
이를 방지한것이 prefix-free code이다.
허프만 코드인 완전이진트리(leaf node가 아니면 무조건 2개의 자식을 갖는것)이다.
어떤 문자열의 속한 문자의 전체 빈도수가 100이라고 할 떄 각 문자들의 빈도수가 아래와 같다고 하자.
a b c d e f 45 13 12 16 9 5 먼저 빈도수가 낮은 순으로 정렬해준다.

그 다음 빈도수가 낮은 두 개를 하나의 이진트리로 만들어 배열에 다시 넣는다.
이 때 작은 수는 오른쪽에 들어가고 큰 수는 왼쪽으로 들어간다.
작은 쪽의 간선은 0이고, 큰쪽은 1이다.
따라서 빈도수가 가장 낮은 f와 e가 합쳐져 새롭게 14로 배열에 들어가게 된다.

또 다시 빈도수를 기준으로 정렬해주고, 빈도수가 가장 낮은 두개를 합쳐준다.
c와 b를 합쳐준다.

다시 정렬해주고 또다시 빈도수가 가장 낮은 두개를 합쳐준다.
14와 d를 합쳐준다

그다음 30과 25를 합쳐준다.
그리고 마지막으로 30과 25를 합친것과 a를 합쳐준다.


우리는 이러한 과정을 저장하는 배열의 자료구조를
priority_queue를 사용하는 것이 좋다 (min heap)
insert와 delete를 할 때 O(log n)을 보장한다.

이를 적용하면 허프만 코드는 시간복잡도가 O(nlogn)이 된다.
Scheduling with Greedy Methods
Minimizing Total Time in the System
T = {t1, t2, t3} = {5, 10, 4} 일 때 적절한 스케줄링을 통해 최소의 시간을 구하는 것이다.
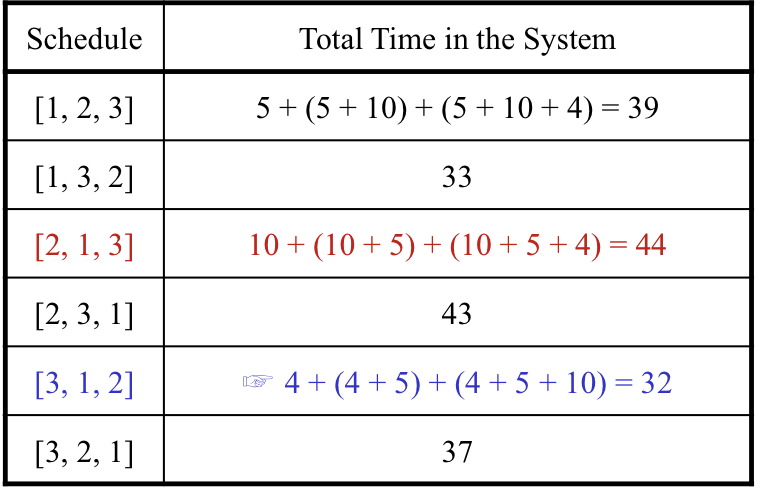
최소 시간은 32가 되고, 최대 시간은 44가 된다.
그리디 알고리즘을 적용해 모든 t를 오름차순으로 정렬해 진행하면 O(nlogn)의 시간복잡도로 해결가능하다.
Minimizing Lateness

job ti 와 di가 주어졌을 때 ti는 소요시간이고 di는 마감기한 시간이다.
예를 들어 t1 = 3, d1 = 6일 때 1번 job은 3시간 걸리고 6시까지 마감해야 한다는 것이다.
만약 마감기한을 넘어버리면 lateness가 발생한다.
즉, lateness를 최소로하는 방법을 찾아야 한다.
위의 예시에서는 1번 job이 2시간 lateness가 발생하였고, 4번 job이 6시간 lateness가 발생하였다.
결국 스케줄링을 {3, 2, 6, 1, 5, 4}로 할경우 6시간의 lateness가 발생한다.

위와 같이 스케줄링을 {1, 2, 3, 4, 5, 6}으로 하면 1시간의 lateness가 발생한다.
EDF알고리즘을 사용해 문제를 해결할 수 있다.
Earliest-Deadline-First algorithm (EDF 알고리즘)
edf알고리즘에는 inversion이 없어야 한다.
inversion이란

마감기한이 빠른 순으로 정렬되어 있는 와중에 마감기한이 느린 job이 마감기한이 빠른 job 보다
앞에 먼저 배치되는 상황을 의미한다.
만약 inversion이 발생했을 경우, inverted된 job 두개는 서로 붙어있어야 한다.

이렇게 되면 결국 어느시점에 가서는 마감기한이 줄어든다.
여기서 만약 j와 i를 swap하면 어떻게 될까?

보시다 시피 swap을 해도 두 job이 끝나는 시간은 동일하다.
따라서 우리는 두 job의 lateness만 신경쓰면 된다.
maximum lateness가 관건이기 때문에 두 job들 중 더 늦는 것에만 초점을 맞추면 된다.
swap 이전에는 i의 lateness가 j의 lateness보다 크니 i가 관건이다.
swap 이후에는 j의 lateness가 i의 lateness보다 크니 j가 관건이다.

따라서
swap 이후의 lateness가 더 작아 지므로 swap을 하는 것이 좋다.

시간 복잡도는 O(nlogn)이 된다.
Scheduling with Deadlines

모든 job은 1시간만에 완료된다.
마감시간 안에 job을 완료하면 profit을 얻을 수 있다.
그렇지 못하면 0을 얻는다.
profit을 최대화하는 것이 목표이다.
해답은 1) profit이 큰 것부터 수행하는 것이다. 2) 정렬된 list에서 각 job을 보면서, 가능한 경우 schedule에
추가한다.

오른쪽의 list는 이미 profit이 큰것대로 정렬해 놓은 것이다.
이를 차례대로 schedule에 집어 넣으면서 확인한다.
시간 복잡도는 O(n^2) 이 된다.
ex)
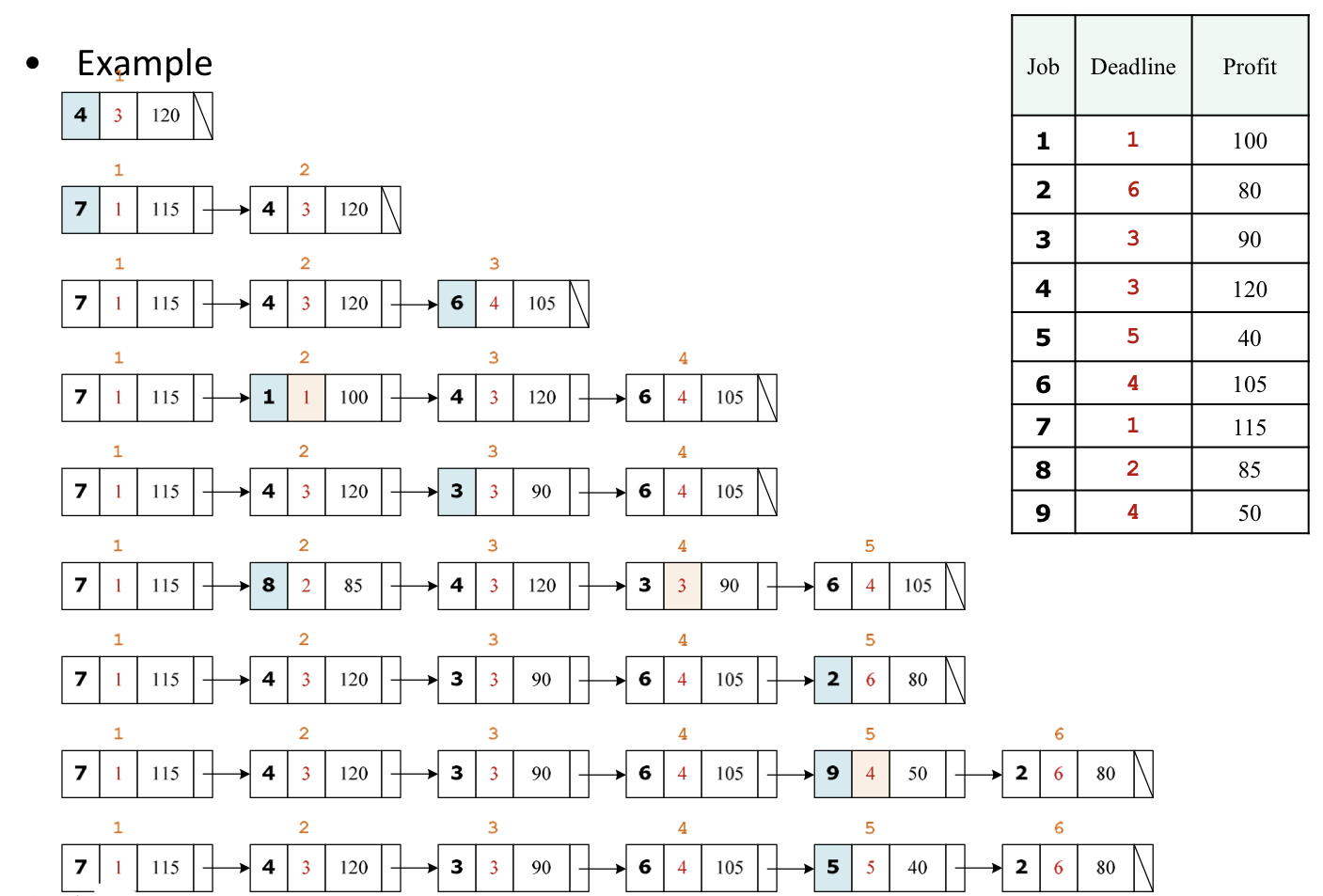
'알고리즘 설계와 분석' 카테고리의 다른 글
Chapter 25 : Matching in Bipartite Graphs (0) 2022.12.19 Chapter 24 : Maximum Flow (0) 2022.12.14 Chapter 3 (0) 2022.10.24 Chpater 1 & 2 (0) 2022.10.24