Chapter 24 : Maximum Flow

Graph

G = (V, E)라고 표현 

V  = 정점, E = 간선

|V| = V집합의 갯수

|E| = E집합의 갯수

예를 들어 V = {1, 2, 3, 4, 5}일 때 |V| = 5 이다.

 

n개의 정점이 있는 그래프에서 최대 간선은 n(n-1) / 2 개이다.

만약 그래프가 n개의 정점이있고 간선은 n(n-1)/2 개 있으면 완전 그래프라고 부른다.

 

그래프의 표현은 2가지가 있다.

1. Adjacency List

2. Adjacency Matrix

 

Adjacency List

공간 복잡도는 O(V + E) 이다.

 

Adjacency Matrix

|V| * |V| 크기의 배열을 생성

공간 복잡도는 O(V^2)

 

Depth First Search (DFS)

한 정점을 계속 깊이 탐색하는 알고리즘 이다. 모든 정점과 간선을 탐색한다.

adjacency list를 사용할 경우 시간복잡도는 O(n+e) 가 된다.

adjacency matrix를 사용할 경우 시간 복잡도는 O(n^2) 이된다.

 

Breath First Search (BFS)

한 정점에서 인접한 정점 부터 방문하는 알고리즘이다.

adjacency list를 사용할 경우 시간복잡도는 O(n+e) 가 된다.

adjacency matrix를 사용할 경우 시간 복잡도는 O(n^2) 이된다.

 

Flow Networks

source(s)에서 sink(t)로 흐를 수 있는 최대 flow를 구하는 알고리즘이다.

각 간선을 방향성이 존재하고 간선의 용량은 capacity(c)라고 한다.

c(Vancouver, Edmonton) = 16 이다.

노드 u와 v사이를 흐르는 flow는  f(u, v)라고 쓰며 

flow는 그 간선의 용량을 초과할 수 없다.

f(u, v) <= c(u, v) 이다.

|f|는 source에서 sink로 흘러가는 flow의 크기이다. 

source에서 나오는 flow는 모두 sink로 흘러가므로 이는 sources에서 나오는 flow의 합과 같다.

아래의 그래프는 |f| = 19 이다.

f(u, v) / c(u, v) 를 표시한 모습이다.

 

The Ford-Fulkerson Method

반복적으로 flow를 늘려주면서 최대 flow를 찾는 알고리즘이다.

먼저 G에 포함된 모든 f(u, v)를 0으로 초기화 해준다.

residual network에 표현된 augmenting path가 없어질때 까지 flow를 늘려준다.

 

Residual Network

현재 flow가 얼만큼 흘렀는가를 표시하는 것이다.

즉, flow의 기록을 남기는 것이다.

기록을 남기기 위해서는 G에 포함되지 않은 간선이 포함될 수 있다.

c(u, v)  = 16이고, f(u, v) = 11이라면

Augmenting Paths

augmenting path인 p는 residual network에서 s에서 t로 갈 수 있는 경로이다.

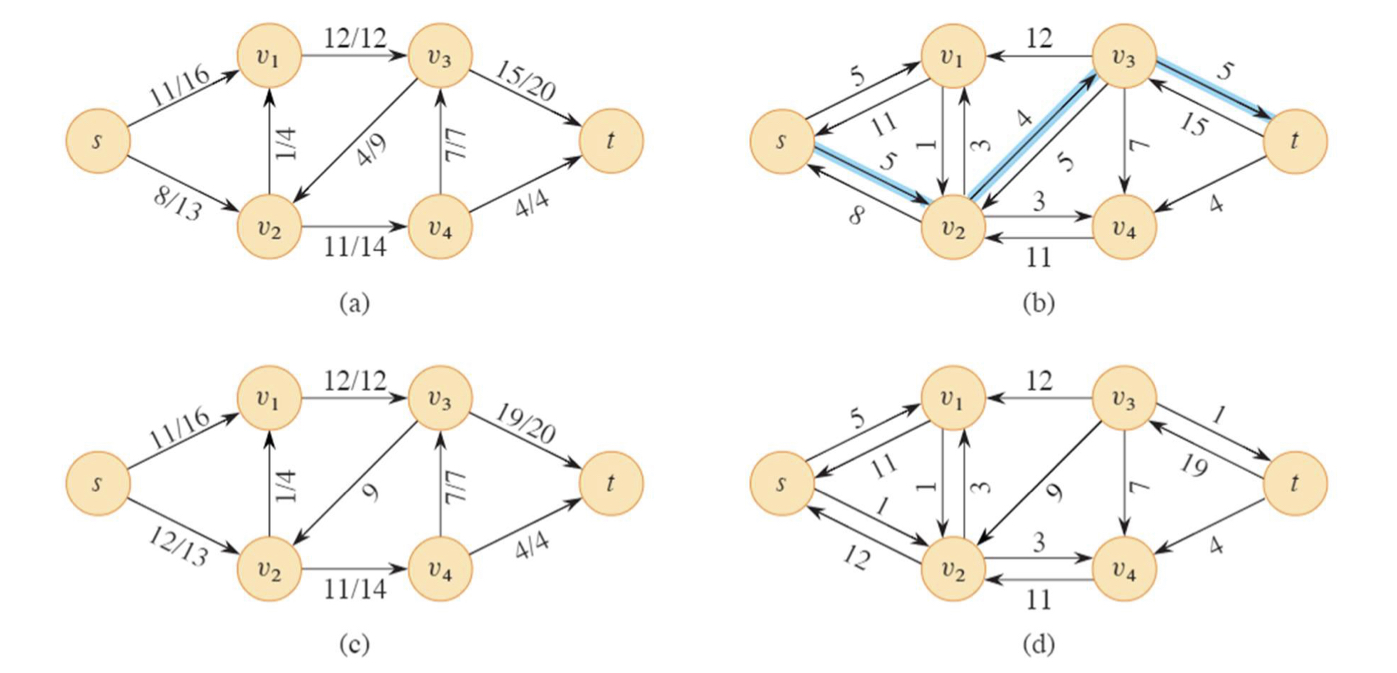
먼저 (a)처럼 residual network가 주어질 때 (b)의 파란색으로 칠해진 augmenting path가 존재한다면

augmenting path중 가장 작은 flow인 4를 흘려준다.

그렇게 되면 (c) 처럼 변하고 이를 residual network로 표현해준것이 (d)이다.

 

이처름 augmenting path가 존재할 때 까지 flow를 늘려줘 결국 이 알고리즘이 끝나면 

maximum flow를 찾았다고 할 수 있는가??

max-flow min cut 정리가 이를 설명한다.

 

Cut

cut이란 network를 정확히 두 개로 쪼개는 것을 의미한다.

쪼갤 때 한쪽에는 s가 속하고 다른쪽에는 t가 속하도록 하는 cut만 고려할 것이다.

cut(S, T)가 있을 때, 이 cut를 가로지르는 flow의 양은 f(v1, v3) + f(v2, v4) - f(v3, v2) 이다.

즉, 12 + 11 - 4  = 19이다.

이 cut의 용량은 c(v1, v3) + c(v2, v4) = 12 + 14 = 26 이다.

 

여기서 중요한 점이 존재한다.

1. cut(S, T)의 flow양은 |f| 이다. 

위의 그래프를 보면 cut(S, T)의 flow는 19이고, |f| 또한 19이다. (|f| = 11 + 8 = 19)

 

2. cut(S, T)의 flow 양 ≤ capacity of cut

위의 그래프를 보면 cur(S, T)의 flow = 19 이고 capacity of cut = 26이다.

 

1과 2를 통해 어떤 flow도 cut capacity의 최솟값보다 많은 flow를 흘릴 수 없다.

따라서 어떤 network에서든 cut capacity는 flow의 상한을 이룬다.

그러므로 만약 우리가, capacity가 가장 작은 cut을 찾는 다면, 이는 flow의 max값을 구하는데 

큰 도움이 될 것이다.

 

3. cut(S, T)중 가장 capacity가 작은 것을 x라고 하자, 그러면 임의의 flow f에 대해, |f| ≤ c(x)를 항상 만족한다.

또한 어떤 flow f와 어떤 cut y가 |f| = c(y)를 만족한다면 f는 maximum flow이고, y는 min cut이다.

 

1, 2번 줄은 f를 0으로 초기화 한다.

while문은 augmenting path인 p를 찾고, f를 계속해서 증가시키고, residual을 만든다.

6 ~ 8번째 줄은 residual 을 업데이트 하는 과정이다.

augmenting path가 없을 경우, f는 maximum flow이다.

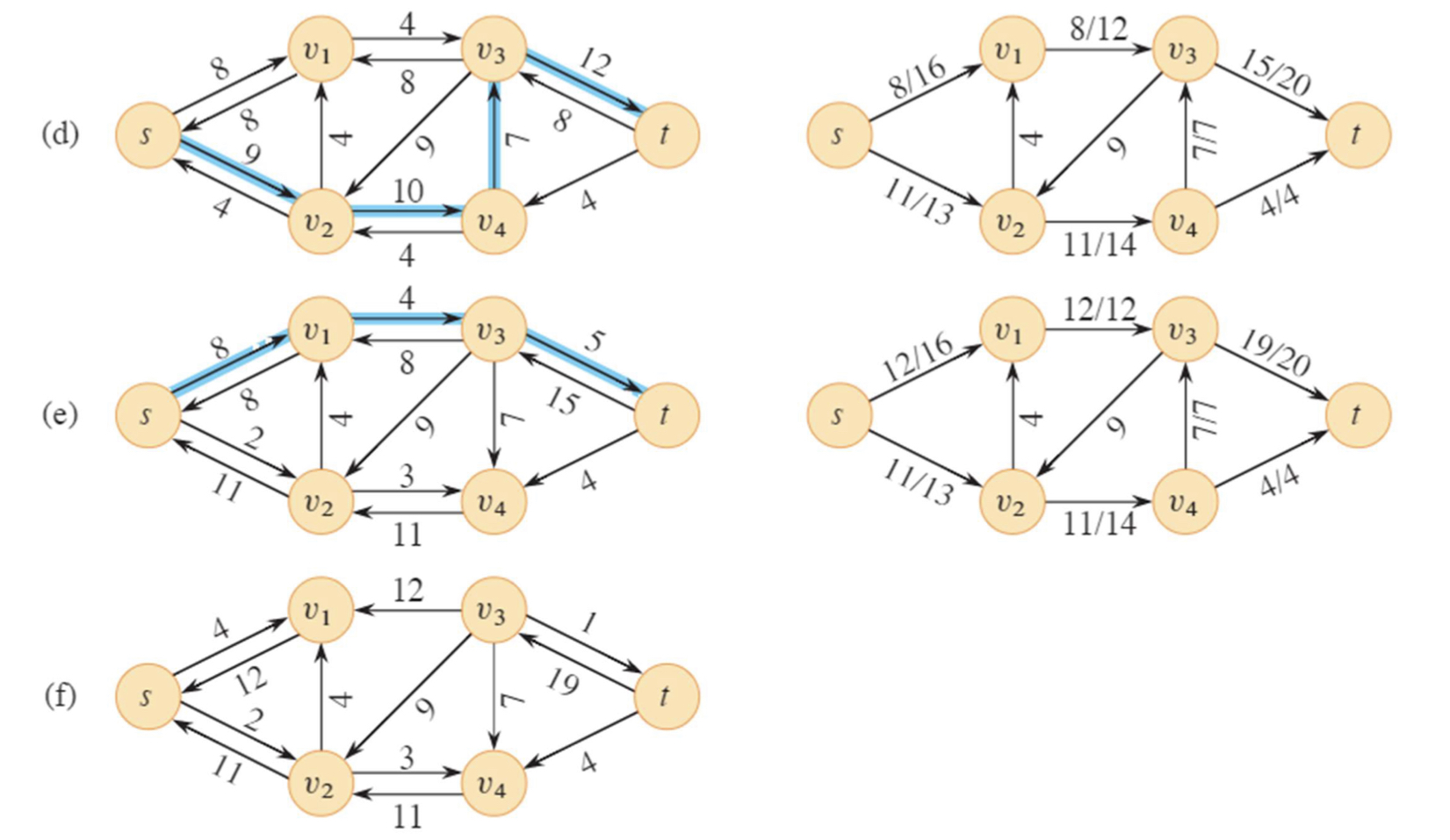
fort-fulkerson의 시간복잡도는 maximum flow인 f에 대해서 augmenting path를 찾기 위해

dfs나 bfs를 이용하므로 O(|V| + |E|) = O(|E|)

최대 f번 탐색하므로 |f*| 번 진행해줘야 한다. (|f*| = maximum flow)

따라서 O(|E|) * |f*| = O(E|f*|) 이다.

 

The Edmonds-Karp algorithm

ford-fullkerson 알고리즘의 가장 큰 문제점은 augmenting path를 찾을 때 가장 빠른 경로를 찾지

못한다는 것이다. 따라서 exponential 시간에 해결 될 수 도 있다.

항상 shortes path를 찾는 다면 polynomial 시간 만에 해결이 가능할 것이다.

최단 경로는 BFS를 사용해 얻을 수 있다.

시간 복잡도는 O(VE^2) 이다.

 

Maximum Bipartite Matching

가장 많은 matching을 제공한다.

L과 R의 matching 관계를 maximum flow로 치환할 수 있다.

matching이 flow이다.

flow문제에서 augment path를 찾을 수 없을 때 까지 반복했다면 

matching 문제에서 최대로 matching을 찾으면 똑같다.

O(VE)의 시간복잡도를 가진다.