-
백준 11062(카드 게임) JAVA백준 문제 2023. 2. 17. 18:36728x90
11062번: 카드 게임
근우와 명우는 재미있는 카드 게임을 하고 있다. N개의 카드가 일렬로 놓여 있다. 각 카드에는 점수가 적혀있다. 근우부터 시작하여 번갈아가면서 턴이 진행되는데 한 턴에는 가장 왼쪽에 있는
www.acmicpc.net
명우와 근우가 카드게임을 한다.
n개의 카드가 일렬로 주어지면 명우와 근우가 각자의 턴에 카드 양끝쪽 중 1개를 선택해 카드에 쓰여진 점수를
획득할 수 있다.
이 때 명우가 얻는 점수를 구하면됩니다. 항상 명우가 먼저 카드를 뽑습니다. 명우와 근우는 항상 이기기 위해
최선의 카드를 선택합니다.
예를 들어 n = 4이고 카드가 1, 2, 5, 2 이렇게 주어지면
명우가 얻는 점수는 6입니다.
dp로 접근하는 문제인지는 알았지만 점화식을 세우는 데 매우 어려웠습니다.
일단 카드 양끝점중 더 높은 카드를 뽑게 그리디한 방법은 절대 안됩니다.
결국 승리하기 위해서는 미래에 내가 뽑을 카드 까지 다 생각해야 하는데 이는 처음부터 계산 하면 불가능합니다.
따라서 거꾸로 생각 하는 것입니다.
n개의 카드가 있다면, 카드가 1개 남았을 때 부터 n개 남아있을 때까지 거꾸로 계산해주면 됩니다.
dp[i][j] = i번째 카드 부터 j번째 카드가 남아있을 때 명우가 얻을 수 있는 가장 큰 값입니다.
따라서 정답은 dp[1][n]이 됩니다.
n = 4이고 카드는 {1, 2, 5, 2}라고 합시다.
1) 먼저 거꾸로 계산해야 하기 때문에 카드가 1장 남았을 경우를 생각합니다.
즉, dp[1][1], dp[2][2], dp[3][3], dp[4][4]를 생각해 볼 수 있습니다.
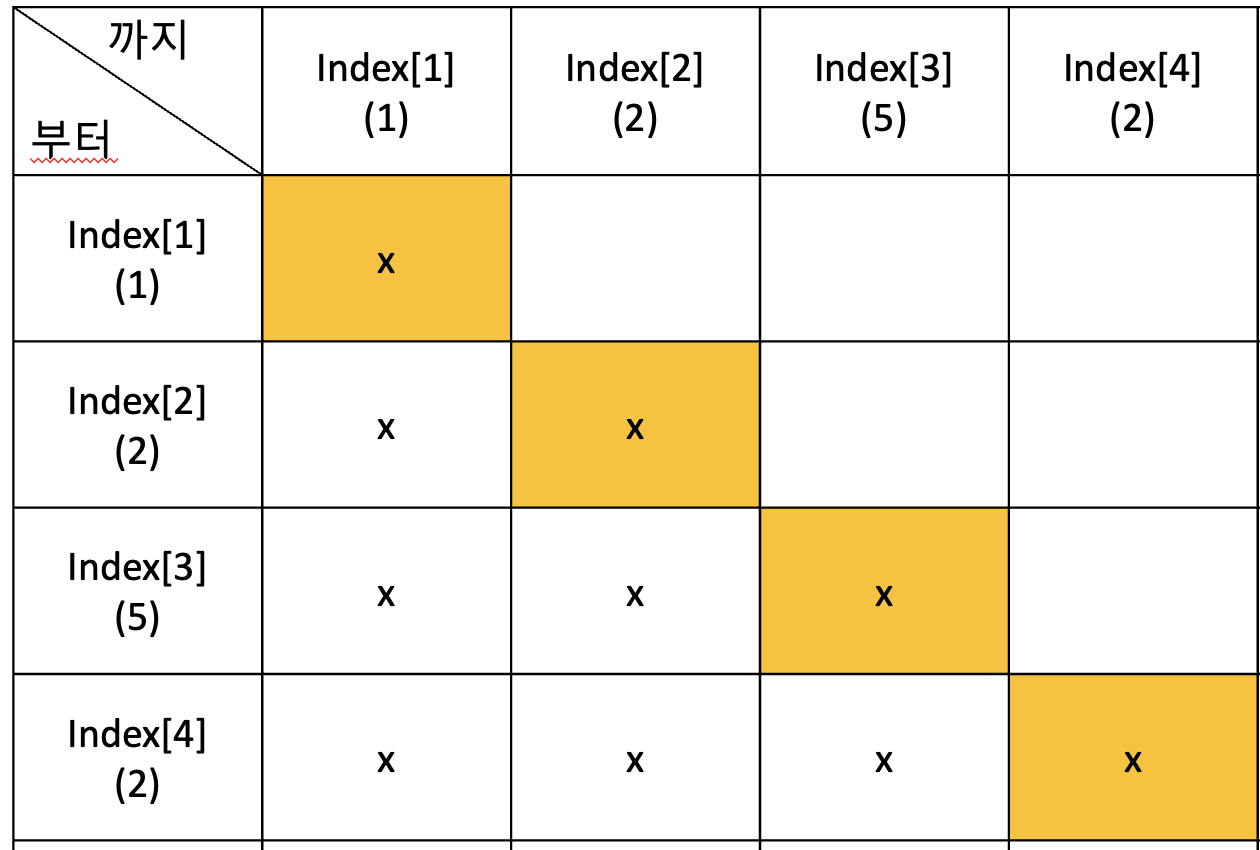
카드가 짝수 이기 때문에 마지막에 뽑을 수 있는 사람은 근우 입니다.
따라서 명우는 카드를 뽑지 못하기 때문에 0입니다.
2)이제 카드가 2장 남았을 경우를 생각합니다.
즉, dp[1][2], dp[2][3], dp[3][4]를 생각할 수 있습니다.

2장남았기 때문에 명우가 뽑을 수 있습니다.
명우는 한장 남았을 때 뽑을 수 있는 카드 중 가장 큰 것 + 지금 내가 뽑을 수 있는 카드중 가장 큰 것을 뽑습니다.
즉, dp[1][2] = max(dp[1][1] + arr[2] , dp[2][2] + arr[1]) 가 됩니다.
나머지 경우도 마찬가지 입니다.
3) 이제 카드가 3장 남았을 경우를 생각합니다.
즉, dp[1][3], dp[2][4]를 생각할 수 있습니다.

3장 남았기 때문에 근우가 뽑을 수 있습니다. (명우는 뽑지 못합니다.)
근우는 자신이 이기기 위해 명우가 작은값을 뽑게 하기 위할 것입니다.
따라서 dp[1][3] = min(dp[1][2], dp[2][3])이 됩니다.
나머지도 동일합니다.
4)이제 카드가 4장남았을 경우를 생각합니다.
즉, dp[1][4]를 생각할 수 있습니다.

4장남았기 때문에 명우가 뽑을 수 있습니다.
아까 2장남았을 경우와 마찬가지로
dp[1][4] = max(dp[1][3] + arr[4], dp[2][4] + arr[1])가 됩니다.
따라서 최종적으로 답은 6이 됩니다.
또 다른 예시도 마찬가지 입니다.
n = 5이고 카드는 {1, 4, 3, 2, 5}일 경우

다음과 같은 dp테이블이 완성됩니다.
int n = sc.nextInt(); int []arr = new int [n+1]; int [][]dp = new int[n+2][n+1]; for(int i =1;i<=n;i++) { arr[i]=sc.nextInt(); }입력 부분입니다.
boolean myengwu=true; if(n%2==0)myengwu=false;n이 짝수이면 근우먼저 계산해 줘야 하고, n이 홀수이면 명우먼저 계산해줘야 합니다.
for(int i=1;i<=n;i++) { for(int j=1;j<=n-i+1;j++) { int row = j; int col = i+j-1; if(myengwu) dp[row][col] = Math.max(dp[row+1][col]+arr[row], dp[row][col-1]+arr[col]); else dp[row][col] = Math.min(dp[row+1][col],dp[row][col-1]); } myengwu = !myengwu; } System.out.println(dp[1][n]);dp테이블을 순회할 때 대각선 방향으로 순회하기 때문에 변수 row와 col을 설정하였습니다.
나머지는 위에서 세웠던 점화식과 동일합니다.
전체 코드입니다.
package hello; import java.util.Scanner; public class Hello { public static void main(String[] args) { int t; Scanner sc = new Scanner(System.in); t = sc.nextInt(); while(t-- > 0) { int n = sc.nextInt(); int []arr = new int [n+1]; int [][]dp = new int[n+2][n+1]; for(int i =1;i<=n;i++) { arr[i]=sc.nextInt(); } boolean myengwu=true; if(n%2==0)myengwu=false; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)dp[i][j]=0; for(int i=1;i<=n;i++) { for(int j=1;j<=n-i+1;j++) { int row = j; int col = i+j-1; if(myengwu) dp[row][col] = Math.max(dp[row+1][col]+arr[row], dp[row][col-1]+arr[col]); else dp[row][col] = Math.min(dp[row+1][col],dp[row][col-1]); } myengwu = !myengwu; } System.out.println(dp[1][n]); } } }'백준 문제' 카테고리의 다른 글
백준 1072번(게임) c++ (0) 2023.03.07 백준 2342(Dance Dance Revolution) c++ (0) 2023.03.06 백준 5582(공통 부분 문자열) (0) 2023.02.17 백준 7579(앱) c++ (0) 2023.02.16 백준 1516(게임 개발) c++ (0) 2023.02.13