chapter 4-1 : List (정렬, STACK, QUEUE)

Linked list for merge (연결리스트를 이용한 오름차순 정렬 merge)

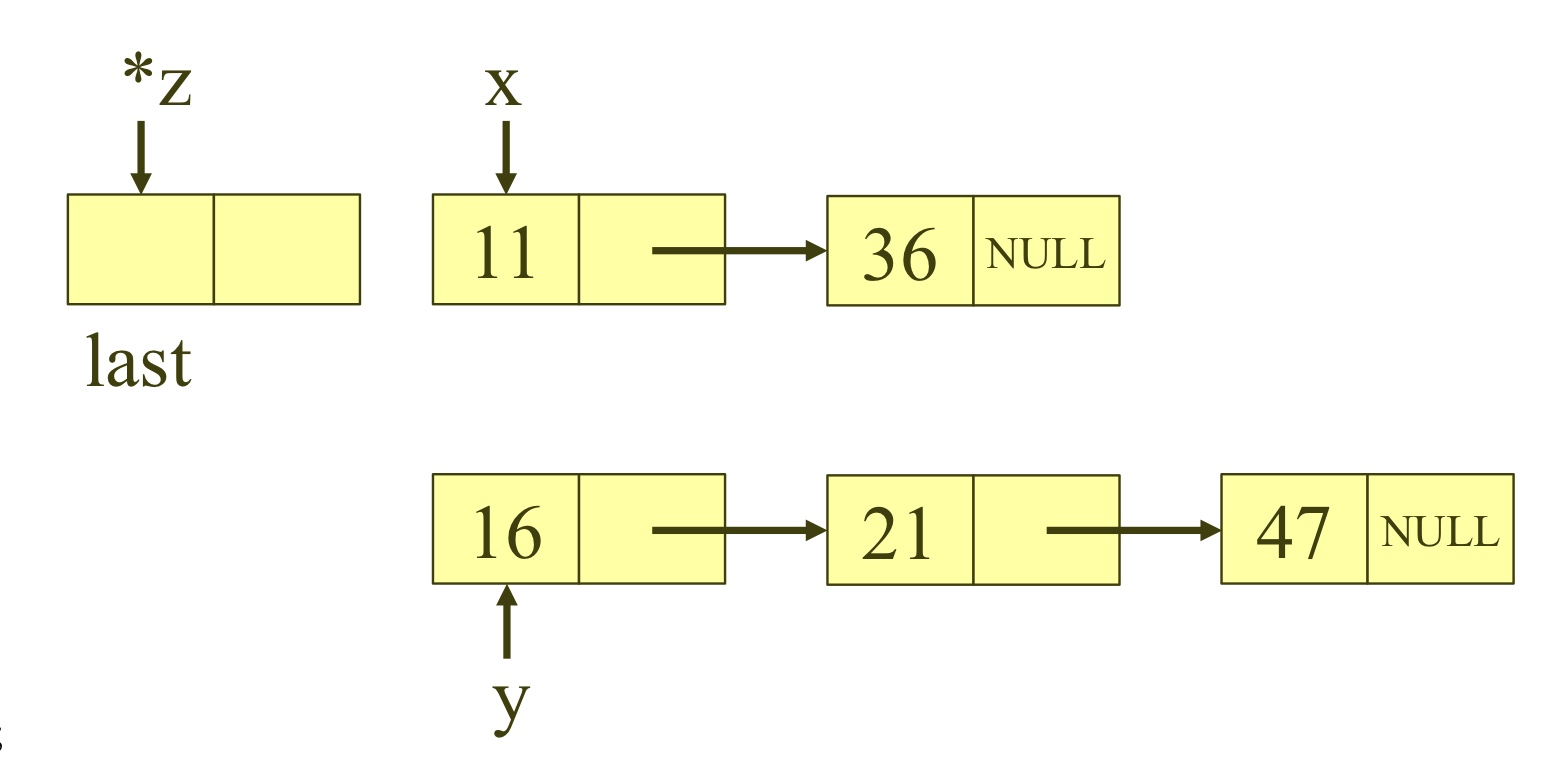
연결리스트 방법을 사용하여 오름차순을 하는 코드 입니다.

X = {11, 36} 이 있고 

Y = {16, 21} 이 있는 상태입니다.

이 둘의 연결리스트들을   합쳐서 오름차순으로

정렬해야 합니다.

typedef struct list_node *list_pointer;
typedef struct list_node {
	int data;
	list_pointer link;
}list_node;
list_pointer ptr = NULL;

연결리스트의 원형입니다.

void merge(list_pointer x, list_pointer y, list_pointer* z) {
	list_pointer last; //노드 맨끝에 포인터 선언
	last = (list_pointer)malloc(sizeof(list_node));
	*z = last;

노드의 임시 맨 뒤에 있는 노드 포인터 last를 선언합니다.

이 last 포인터는 계속해서 X와 Y를 비교해주면서 여러 노드를 가리킵니다. 

두번째 줄에서 last는 현재 리스트의 크기만큼을 가리키는 포인터로 동적할당 됩니다.

*z 는 last를 가리키는 포인터입니다.

while (x && y) {
		if (x->data <= y->data) { 
			last->link = x; //맨 끝을 가리키는 last가 x를 가리킴
			last = x; //last의 data가 x의 data가 됨
			x = x->link; //x가 다음 리스트를 가리킴
		}
		else {
			last->link = y; //맨 끝을 가리키는 last가 y를 가리킴
			last = y; //last의 data가 y의 data가 됨
			y = y->link;//y가 다음 리스트를 가리킴
		}
	}

while절에서는 x와 y가 NULL을 가리키기 전까지 계속 반복됩니다.

그 다음 X가 가리키는 data와 Y가 가리키는 data를 비교해 줍니다.

        if (x) last->link = x; 
	if (y)last->link = y;
	last = *z; *z = last->link; free(last);
}

X와 Y중 먼저 먼저 리스트가 끝난 포인터는 NULL를 가리키고 있으므로 

마지막으로 last가 가리키는 link가 X나 Y를 가리키고 

맨 마지막 코드를 보면 last는 맨 뒤에 있는 *z가 가리키는 node가 되고

*z는 last가 가리키는 link 즉, 진짜 병합된 리스트들의 맨뒤를 가리키게 됩니다.

마지막으로 free함수를 이용해 아까  처음에 malloc을 사용한 메모리를 삭제합니다.

맨 마지막 코드 

---

Linked Stacks and Queues (연결리스트 스택 과 큐)

LIST STACK (PUSH, POP)

#define MAX_STACKS 10
typedef struct {
	int key;
	//기타
}element;
typedef struct stack* stack_pointer;
typedef struct stack {
	element data;
	stack_pointer link;
}stack;
stack_pointer top[MAX_STACKS];

구조체 element는 스택의 data입니다. 여기에다가 정보를 넣습니다.

stack_pointer는 stack 노드를 가리키는 포인터입니다.

포인터 배열 top은 각각 top i번째 stack 노드를 가리킵니다.

처음에 top[i]는 NULL을 가리킵니다.

i 번째 스택이 공백이면 top[i] = NULL 입니다.

 

먼저 PUSH 함수 부터 살펴 보겠습니다.

main 함수에서 push(i, item)을 수행하면

void push(int i, element item) {
	stack_pointer temp = (stack_pointer)malloc(sizeof(stack));
	if (IS_FULL(temp)) {
		fprintf(stderr, "The memory is full\n");
		exit(1);
	}
	temp->data = item;
	temp->link = top[i];
	top[i] = temp;
}

temp라는 새로운 item을 저장할 노드를 선언합니다.

if문에서는 만약 stack의 가득 차있을때 수행합니다.

임의의 temp의 data가 item이 되고 링크(포인터)가 top[i]가 원래 가리키던 노드를 가리킵니다.

마지막 코드는 top[i]가 새로들어온 temp노드를 가리킵니다.

 

POP 함수를 살펴보겠습니다.

main 함수에서 item = pop(i)를 수행하면

element pop(int i) {
	stack_pointer temp = top[i];
	element item;
	if (IS_EMPTY(temp)) {
		fprintf(stderr, "The stack is empty\n");
		exit(1);
	}
	item = temp->data;
	top[i] = temp->link;
	free(temp);
	return item;
}

임의의 노드 temp는 원래 top[i]의 노드로 복사됩니다.

element 형 item을 선언했는데, top[i]의 data를 저장하기 위함입니다. 마지막에 return해줍니다.

if문은 top[i]가 비어있으면 수행해줍니다.

나머지 코드는 밑의 사진을 통해 설명됩니다.

 

LIST QUEUE (PUSH, POP)

#define MAX_QUEUES 10
typedef struct {
	int key;
	//기타
}element;
typedef struct queue* queue_pointer;
typedef struct queue {
	element data;
	queue_pointer link;
}queue;
queue_pointer front[MAX_QUEUES], rear[MAX_QUEUES];

구조체 element는 queue의 data입니다.

스택과 다른점은 포인터 배열이 front, rear 총 2개라는 점입니다.

큐는 들어올때는 뒤에서 앞으로 계속 들어오게 됩니다.

나갈때는 앞에서 부터 나가게 됩니다.

따라서 front 와 rear의 포인터를 통해 push함수와 pop함수를 수행해 줍니다.

초기에는 front[i] =NULL 입니다.

i번째 큐가 공백이면, front[i]=NULL입니다.

 

먼저 PUSH함수부터 살펴보겠습니다.

main 함수에서 addq(i, item)를 수행해주면

void addq(int i, element item) {
	queue_pointer temp = (queue_pointer)malloc(sizeof(queue));
	if (IS_FULL(temp)) {
		fprintf(stderr, "The memory is full\n");
		exit(1);
	}
	temp->data = item;
	temp->link = NULL;
	if (front[i])rear[i]->link = temp;
	else front[i] = temp;
	rear[i] = temp;
}

새로 들어올 data를 저장할 temp 노드를 만들어 줍니다.

temp의 data에 item을 넣어주고 link는 NULL을 가리키게 해줍니다.

왜냐하면 큐의 데이터가 들어오면 맨 마지막 끝에 들어오게 되기 때문입니다.

if문에서 front[i]가 가리키는 노드가 있으면 rear[i]의 link를 temp에 연결해 줍니다.

else문에서는 front[i]가 가리키는 노드가 없다는 의미이므로 바로 temp를 넣어줍니다.

마지막으로 rear[i]는 temp를 가리킵니다.

 

POP 함수를 살펴보겠습니다.

main함수에서는 item = deleteq(i) 를 수행해주면

element deleteq(int i) {
	queue_pointer temp = front[i];
	element item;
	if (IS_EMPTY(temp)) {
		fprintf(stderr, "The stack is empty\n");
		exit(1);
	}
	item = temp->data;
	front[i] = temp->link;
	free(temp);
	return item;
}

어차피 queue에서도 pop을 해줄때 맨 앞에 data를 빼주므로 deleteq함수도 stack의 pop함수와 똑같습니다.