Chapter 5-1 : Tree (Binary Tree Traversal 이진 트리 순회)

순회 알고리즘이란 tree의 각 node를 한번씩 방문하는 알고리즘입니다.

typedef struct node* treepointer; //노드를 가리키는 포인터
typedef struct node { //노드생성
	int data;
	treepointer left, right; //노드의 오른쪽,왼쪽을 가리키는 포인터
}node;

 

Inorder 중위 순회

왼쪽 branch(가지)를 모두 방문한 후 node를 방문하고 오른쪽 branch를 방문합니다.

다음 그림에서 보면 중위순회를 하게 되면 output은 A / B * C * D + E가 됩니다.

void inorder(treepointer ptr) { //중위 순회
	if (ptr) {
		inorder(ptr->left); //왼쪽 자식 먼저
		printf("%d", ptr->data); // 정점 출력
		inorder(ptr->right);
	}
}

---

Preorder 전위순회

node를 방문하고 왼쪽 branch를 모두 방문한 후 오른쪽 branch를 방문합니다.

다음 그림에서 보면 전위순회를 하게 되면 output은 + * * / A B C D E 가 됩니다.

void preorder(treepointer ptr) { //전위 순회
	if (ptr) {
		printf("%d", ptr->data); //먼저 정점 출력
		preorder(ptr->left); //왼쪽먼저
		preorder(ptr->right);
	}
}

---

Postorder 후위순회

왼쪽 branch를 모두 방문하고 오른쪽 branch를 방문한 후 node를 방문합니다.

다음 그림에서 보면 후위순회를 하게 되면 output은 A B / C * D * E + 가 됩니다.

void postorder(treepointer ptr) { //후위 순회
	if (ptr) {
		postorder(ptr->left); //왼쪽 자식 먼저
		postorder(ptr->right);
		printf("%d", ptr->data); // 정점 출력
	}
}

---

Iterative Inorder Traversal

방금전에 배웠던 inorder(중위순회)를 Stack형식으로 구현하는 것입니다.

1) 왼쪽 node부터 계속 stack에 쌓여지기 시작합니다. 만약 node가 NULL이면 stack에 쌓는걸 멈춥니다.

2) NULL 에 도착하기 전에 stack에 쌓여있던 top node를 stack에서 제거해주고 그 제거된 노드의 오른쪽 node를 

stack에 쌓습니다.

void iter_inorder(treepointer node) {
	int top = -1; //stack 초기화
	treepointer stack[MAX_STACK_SIZE];
	for (;;) {
		for (; node; node = node->left)
			push(node); //스택에 쌓기
		node = pop(); //가장 높은 stack의 노드 제거
		if (!node) break; //NULL 이면 멈춤
		printf("%d", node->data);
		node = node->right;
	}
}

위의 node를 기준으로 보면 

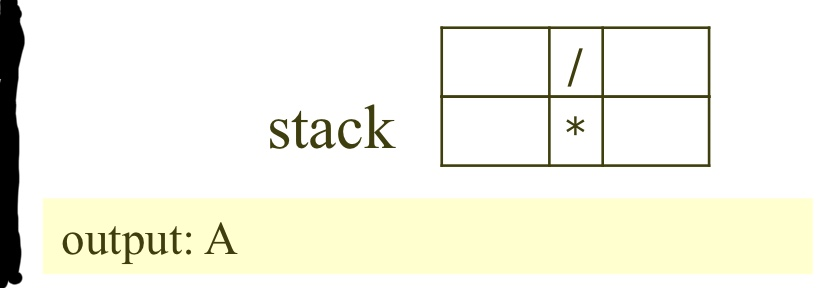
그 다음 stack에는 B가 들어옵니다.

이러한 알고리즘이 반복 되면

output은 A / B * C 가 됩니다.

---

Level Order Traversal

트리의 레벨 순서대로 순회하는 알고리즘입니다.

...........................LEVEL 1

 

...........................LEVEL 2

 

...........................LEVEL 3

 

...........................LEVEL 4

 

...........................LEVEL 5

 

1) 먼저 해당 root node를 방문합니다.

2) root node의 left node를 방문합니다.

3) root node의 right node를 방문합니다.

해당 트리로 output를 보면 + * E * D / C A B 입니다.

 

우리는 이러한 알고리즘을 QUEUE로 구현할 것입니다.

void level_order(treepointer ptr) {
	int front = 0; //큐의 앞
	int rear = 0; //큐의 뒤
	treepointer queue[MAX_QUEUE_SIZE];
	if (!ptr) return; 
	addq(ptr); //먼저 맨위의 root node 큐에 삽입
	for (;;) {
		ptr = deleteq();
		if (ptr) {
			printf("%d", ptr->data);
			if (ptr->left) //왼쪽 node 큐에 삽입
				addq(ptr->left);
			if (ptr->right) //오른쪽 node 큐에 삽입
				addq(ptr->right);
		}
		else break;
	}
}

다음과 같은 알고리즘으로 반복됩니다.

---

전체 기본적인 트리 코드 입니다.

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int number = 15; //노드의 갯수
typedef struct node* treepointer; //노드를 가리키는 포인터
typedef struct node { //노드생성
	int data;
	treepointer left, right; //노드의 오른쪽,왼쪽을 가리키는 포인터
}node;
void preorder(treepointer ptr);
void inorder(treepointer ptr);
void postorder(treepointer ptr);
int main() {
	node nodes[16]; //노드들이 들어갈수 있는 노드 배열 선언

	for (int i = 1; i <= number; i++) {
		nodes[i].data = i;
		//먼저 각 포인터에 널값 넣어줌(아직 노드들만 생성되고 서로 이어지지않음)
		nodes[i].left = NULL;
		nodes[i].right = NULL;
	}

	for (int i = 2; i <= number; i++) { //노드를 서로 이어주는 작업
		if (i % 2 == 0) { //노드 번호가 짝수
			nodes[i / 2].left = &nodes[i]; //짝수는 왼쪽
		}
		else { //노드 번호가 홀수
			nodes[i / 2].right = &nodes[i]; //홀수는 오른쪽
		}
	}
	preorder(&nodes[1]);





	return 0;
}
void preorder(treepointer ptr) { //전위 순회
	if (ptr) {
		cout << ptr->data << ' '; //먼저 정점 출력
		preorder(ptr->left); //왼쪽먼저
		preorder(ptr->right);
	}

}
void inorder(treepointer ptr) { //중위 순회
	if (ptr) {
		inorder(ptr->left); //왼쪽 자식 먼저
		cout << ptr->data << ' '; // 정점 출력
		inorder(ptr->right);
	}

}
void postorder(treepointer ptr) { //후위 순회
	if (ptr) {
		postorder(ptr->left); //왼쪽 자식 먼저
		postorder(ptr->right);
		cout << ptr->data << ' '; // 정점 출력
	}

}