Chapter 5-3 : Tree (Heaps)

heap 자료구조는 크게 두 가지로 나뉘어 집니다.

max heap 과 min heap 이 있습니다.

 

Max heap

루트 노드가 자식 노드보다 큰 경우 입니다.

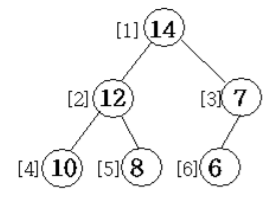
이러한 heap의 자료구조는 우선 순위 큐(Priority Queue) 에서 사용됩니다.

우선 순위 큐는 일반적인 큐와 달리 우선순위에 해당하는 값이 큐의 맨 앞에 위치하고 삭제할때도 가장 먼저

삭제 됩니다.

우선순위는 사용자에 따라 설정할 수 있는데 (max, min) 등 다양하게 설정 가능합니다.

따라서 뒤에 설명할 예시는 max 우선순위 큐를 heap 자료구조로 구현한 예시 입니다.

#define MAX_ELEMENTS 200 
#define HEAP_FULL(n) (n==MAX_ELEMENTS-1)
#define HEAP_EMPTY(n) (!n)
typedef struct {
	int key;
}element;
element heap[MAX_ELEMENTS];
int n = 0; //priority queue 인덱스

기본적인 구조입니다.

구조체 element에는 원하는 원소를 집어 넣으면 됩니다.

 

Insertion into a max heap (max heap에 원소 삽입)

오른쪽에 있는 자료구조에 21을 삽입해보겠습니다.

결론부터 말하면 21은 가장 위에 있는 루트 노트 20 보다 크므로

맨 위에 위치하여야 합니다.

맨 아래 단계의 노드에서 위의 노드까지 계속 비교해주면서 

올라옵니다.

이제 코드를 보겠습니다.

 

 

void push(element item, int* n) {
	int i;
	if (HEAP_FULL(*n)) {
		fprintf(stderr, "The heap is full.\n");
		exit(EXIT_FAILURE);
	}
	i = ++(*n);
	while ((i != 1) && (item.key > heap[i / 2].key)) {
		heap[i] = heap[i / 2];
		i /= 2;
	}
	heap[i] = item;
}

heap은 인덱스 번호 1부터 시작합니다. 따라서 가장큰수는 heap[1] 입니다.

n은 큐의 인덱스 번호입니다. 위의 그림에서 인덱스가 5까지 있으므로 n은 현재 5입니다.

n은 전역변수 이므로 int *n 으로 parameter로 받습니다.

i는 heap의 인덱스 번호 역할을 합니다.

따라서 처음에 들어올 element item을 heap의 가장 뒤에 있는 인덱스 번호에 위치시킵니다. 

while 절에서는 element item을 비교해주면서 들어갈 최적의 인덱스 번호를 갖게 합니다.

마지막 코드를 보면 while절을 끝낸 i는 올바른 인덱스 번호이므로 그곳에 item을 집어넣어 주면 됩니다.

---

Deletion From A Max Heap

결론부터 말하면 왼쪽에 있는 tree가 오른쪽에 있는 tree로 되면 됩니다.

max heap에 pop을 하게 되면 heap[1] = 20 이 삭제되고 나머지 tree들이 재배치 됩니다.

element pop(int* n) {
	int parent, child;
	element item, temp;

	if (HEAP_EMPTY(*n)) {
		fprintf(stderr, "The heap is empty\n");
		exit(EXIT_FAILURE);
	}
	item = heap[1];
	temp = heap[(*n)--];
	parent = 1; child = 2;
	while (child <= *n) {
		if ((child < *n) && (heap[child].key < heap[child + 1].key))
			child++;
		if (temp.key >= heap[child].key)break;
		heap[parent] = heap[child];
		parent = child;
		child *= 2;
	}
	heap[parent] = temp;
	return item;
}