#11 우선순위 큐 & 다익스트라

Priority Queue(우선순위 큐)

우선순위가 가장 높은 원소부터 pop되는 큐

 

ex)원소의 값이 클수록 우선순위가 높다

배열로 구현

1) 삽입 : O(N) / 삭제 : O(1)

2) 삽입 : O(1) / 삭제 : O(N)

결국 둘다 O(N^2)이 걸린다.

 

따라서 힙(Heap)으로 구현

 

Heap (힙)

완전 이진 트리로 이루어진 자료구조

최솟값 or 최댓값을 빠르게 구하기 위한 자료구조

 

최대 힙(Max Heap) : 부모 노드의 값이 자식 노드의 값보다 항상 크거나 같은 힙

최소 힙(Min Heap) : 부모 노드의 값이 자식 노드의 값보다 항상 작거나 같은 힙

느슨한 정렬상태(반 정렬 상태) 유지

 

ex) 최대 힙 (Max Heap)

Heap 원소 삽입 (ex : max heap)

시간 복잡도 : O(log N) 

트리의 높이가 log N이기 때문

 

Heap 원소 삭제 (ex : max heap)

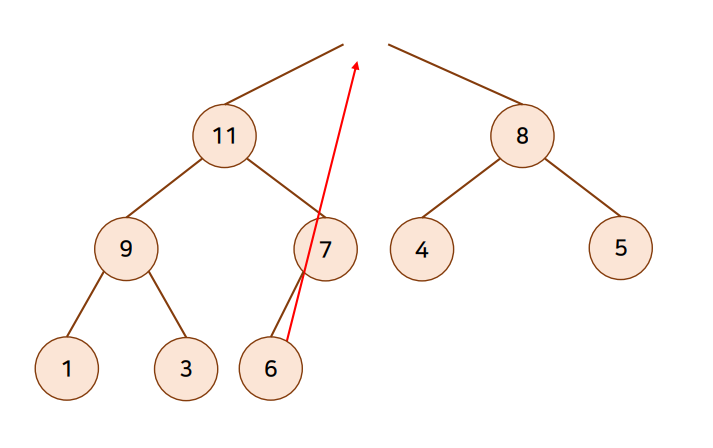
이제 6은 11과 8 둘중 하나와 swap을 해야합니다. 

max heap이기 때문에 11과 swap합니다.

마찬가지로 6은 9와 7중에 9와 swap해줍니다.

시간 복잡도 : O(log N)

 

이러한 Priority Queue는 C++ STL에서 사용 가능합니다.

template<//우선순위 큐 기본 탬플릿
	class T, 
	class Container = std::vector<T>,
	class Compare = std::less<typename Container::value_type> //내림차순(큰 값부터 pop)
>class priority_queue;
//T : 원소의 타입
//Container : priority_queue 의 구현에 사용되는 컨테이너 
//Compare : 우선순위 기준

C++ STL에 있는 기본 템플릿입니다. 

내림차순 형태로 들어가게 됩니다.

priority_queue<int>qp; 
//우선순위 큐 <int>형으로 선언
priority_queue<int,vector<int>>qp; 
//우선순위 큐 <int>형 벡터로 선언
priority_queue<int, vector<int>,greater<int>>qp; 
//우선순위 큐 <int>형 벡터 오름차순으로 선언(작은 값부터 pop)

 

여기서 주의해야 할 점이

greater<int> (비교 클래스) 와 greater<int>() (비교 함수)는 다릅니다.

priority_queue<int,vector<int>,greater<int>> : 작은 원소부터 pop(오름차순)
sort(v.begin(),v.end(),greater<int>()) : 내림차순 정렬

struct cmp { //비교 클래스 (우선 순위 큐에서 사용가능)
	bool operator()(point p1, point p2) {
		if (p1.y == p2.y)return p1.x < p2.x;
		else return p1.y < p2.y;
	}
 };

bool cmp(point p1, point p2) { //비교 함수 (우선 순위 큐에서는 쓸 수 없음)
	if (p1.y == p2.y) return p1.x > p2.x;
	else return p1.y > p2.y;
}

우선순위 큐에는 struct cmp가 들어가야 합니다. (비교 클래스이기 때문)

우리가 평소 사용하는 sort함수에는 bool cmp가 들어갑니다. 

struct point {
	int x;
	int y;
	int z;
};

priority_queue<point, vector<point>, cmp>pq;

pq.push({ 1,2,3 });
pq.push({ 1,1,1 });
pq.push({ 2,6,4 });
pq.push({ 0,2,3 });
while (!pq.empty()) {
	auto [x, y, z] = pq.top();
	cout << x << ' ' << y << ' ' << z << '\n';
	pq.pop();
}
//2 6 4
//1 2 3
//0 2 3
//1 1 1

---

Dijkstra (다익스트라 알고리즘)

최단 경로 탐색 알고리즘

시작점으로 부터 다른 모든 점까지의 최단 거리를 구하는 문제

 

BFS와의 차이점

BFS : 간선의 가중치가 모두 1

다익스트라 : 간선의 가중치가 음이 아닌 값

 

1) 시작점의 거리를 0, 나머지 정점까지의 거리를 최대(MAX)로 설정

2) 아직 방문하지 않은 정점 중 거리가 가장 짧은 정점을 방문 (처음엔 시작점 방문)

3) 인접한 정점 중 아직 방문하지 않은 정점들의 거리 갱신

4) 2~4 반복

초기 모습입니다.

갱신된 정점은 현재 방문한 정점입니다.

처음에 시작점 1의 거리를 0으로 만들어 줍니다.

시작점(1) 과 인접한 2, 3, 4의 거리를 update해줍니다.

 4번 노드의 거리가 가장 짧으므로 4부터 방문해줍니다.

4와 인접한 노드의 거리를 또 update해줍니다. 

처음에 3번 노드로 가는 거리는 1 -> 3 = 10 이었지만 1 -> 4 -> 3 = 5 이기 때문에

5로 update해 줍니다.

4번 노드에서 3번 노드로 가는 거리가 가장 짧으므로 3을 방문해줍니다.

나머지 과정은 계속 똑같습니다.

최종 결과 입니다.

 

시간복잡도 : 

아직 방문하지 않은 정점 중 거리가 가장 짧은 정점 찾기 = O(V)

정점을 방문하는 횟수 = O(V)

Total = O(V^2)

시간이 많이 걸리므로 거리가 가장 짧은 정점을 찾는 과정에서 효율적으로 시간을 줄일 수 있습니다.

바로 Priority_Queue를 사용하는 방식 입니다. O(log N)

 

각 정점은 한 번씩 방문하고 인접한 간선들을 모두 체크

모든 간선을 한 번씩 체크함 (양방향 간선인 경우 2번) -> O(|E|)

Priority_Queue에 보관되는 원소의 최대 개수 -> O(|E|)

=> O(|E|log|E|)

 

구현

5번째 줄은 먼저 모든 그래프의 거리를 MAX로 초기화하는 부분입니다.

7번째 줄은 시작점 S의 거리는 항상 0이기 때문입니다.

9 ~ 25번째 줄부터 BFS 형식으로 Priority_queue를 이용해 인접한 정점까지의 거리중 작은 값먼저 방문하는 형식으로

알고리즘이 진행됩니다.

10번째 줄을 보면 pq.top().first(거리) 에다가 -(마이너스)를 붙였습니다. 

왜냐하면 현재 priority_queue는 내림차순(max heap) 형식으로 되있습니다. 따라서 pop을 할때마다 거리의 최댓값이

나오게 됩니다. 이를 반대로 -를 붙여주면 최솟값이 나오게 됩니다.

만약 -연산이 싫으면 처음부터 priority_queue<int, vector<int>, greater<int>>pq 라고 선언해 줘야 하는데

귀찮습니다.

 

16 - 25번째 줄은 현재 방문한 정점 u와 인접한 정점 들을 priority_queue에 넣어주는 작업니다.

19번째 줄을 보면 현재 내가 방문할 정점(v)의 거리가 현재 방문한 정점의 거리 + v 까지의 거리 보다 크면

update해줘야 하므로 priority -queue에 넣습니다.

21번째 줄을 보면 넣을 때 거리에다가 -를 붙여서 넣어줍니다.

위의 식을 c++ auto를 사용해 조금더 짧은 코드로 나타내었습니다.

 

다익스트라 알고리즘의 주의할 점

1) 음의 가중치를 갖는 간선이 존재하면 안된다. (cycle이 생길 수 있습니다.)

음의 가중치를 구하는 알고리즘은 벨만포드 알고리즘이 따로 존재합니다. 공부하면 좋습니다.

2) 최장거리를 구하는 문제에는 사용할 수 없다

3) 잘못된 코드 구현 조심 (14번째 줄 코드 주의 , c++ auto에서는 8번째 줄)