백준 2423 (전구를 켜라)

문제

2423번: 전구를 켜라

N * M의 직사각형이 주어진다.

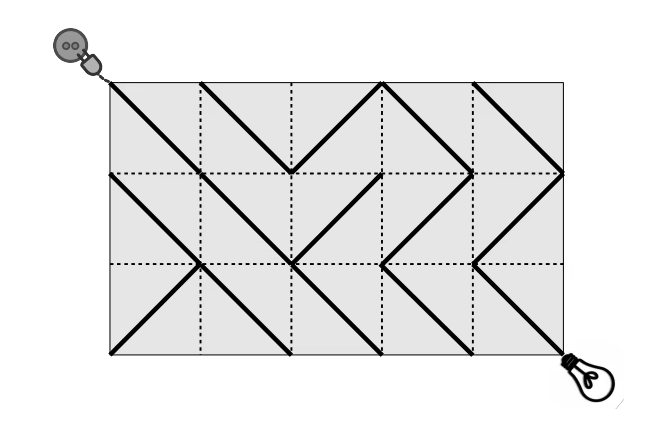
또한 전선의 정보도 위와 같이 주어진다. 여기서 전선은 90도 회전할 수 있다.

이때 맨 왼쪽 상단에서 부터 시작해서 맨 오른쪽 하단에 도달할 때 전선의 회전횟수가 최소로 가게끔 하여 맨 아래 우측에 도달하는 

전선의 최소 회전횟수를 구하는 문제이다.

위 예시에서 보면 4번째 열에 해당하는 모든 전선들은 90도 회전하면 전구에 도달할 수 있다.

---

입력

3 5
\\/\\
\\///
/\\\\

 

정답

1

---

여기서 입력이 위와 같이 / 나 \ 로 주어지기 때문에 이것을 어떻게 그래프 형태로 구현해야 할지 막막했다.

또한 어떤 알고리즘을 사용해야 최소의 회전횟수를 구할 수 있을까?

 

바로 "다익스트라 알고리즘" 이다.

현재 맨 왼쪽 상단에 전선을 회전하지 않고 도달할 수 있는 모든 점은 cost가 0이 되고, 전선을 회전해야지 도달할 수 있는 점은 cost가 1이 된다.

이러한 정보를 저장해 다익스트라 알고리즘을 활용하면 문제를 해결할 수 있다.

 

먼저 우리가 사용할 새로운 클래스를 정의해주었다.

class Path implements Comparable<Path>{
    int nxt; //다음에 갈 노드 번호
    int cost; //다음에 갈 노드까지 cost
    Path(int nxt, int cost){
        this.nxt = nxt;
        this.cost = cost;
    }

    @Override
    public int compareTo(Path p){ //cost를 기준으로 오름차순 정렬
        return this.cost - p.cost;
    }
}

 

입력 부분이다.

private static List<Path>[]list;
list = new List[360001];
for(int i=0;i<=360000;i++)list[i] = new ArrayList<>();

for(int i=1;i<=n;i++){
        String s = br.readLine();
        for(int j=1;j<=m;j++){
           	if(s.charAt(j-1) == '/'){
                addEdge(hash(i-1, j), hash(i, j-1), 0); //정상인 경우
                addEdge(hash(i-1, j-1), hash(i, j), 1); //회전시켰을 경우
            }
            else{ // \인 경우
                addEdge(hash(i-1, j-1), hash(i, j), 0);
                addEdge(hash(i-1, j), hash(i, j-1), 1);
            }
        }
    }
        
private static int hash(int x, int y){
    return x*555+y;
}
 
private static void addEdge(int s, int e, int cost){
    Path p1 = new Path(e, cost);
    list[s].add(p1);

    Path p2 = new Path(s, cost);
    list[e].add(p2);
}

우리는 좌표를 입력받기 때문에 좌표를 어떤 유일한 수로 다시 표현해주어야 한다. 그래야 다익스트라를 하기 편하다.

이러한 일을 하는 함수는 hash(i, j) 이다.

N과 M이 최대 500이기 때문에 유일한 값을 선정했다.

또한 for문을 돌릴 때 i = 1, j = 1부터 시작했다. i = 0부터 돌리면 hash값이 0이 들어갈 수 있어 유일한 값을 보장하지 못한다.

따라서 (1, 1) 부터 시작해서 계속해서 도는 것이다.

 

다익스트라 부분이다.

	int[]dist = new int[360001];
        Arrays.fill(dist, Integer.MAX_VALUE);
        PriorityQueue<Path>pq = new PriorityQueue<>();
        Path p = new Path(0, 0);
        pq.add(p);

        dist[0]= 0;
        while(!pq.isEmpty()){
            int cur = pq.peek().nxt;
            int cost = pq.peek().cost;
            pq.remove();

            if(cost > dist[cur])continue;
            for(Path temp : list[cur]){
                if(dist[temp.nxt] > cost+temp.cost){
                    dist[temp.nxt] = cost+temp.cost;
                    Path t = new Path(temp.nxt, dist[temp.nxt]);
                    pq.add(t);
                }
            }
        }

여기 부분은 평소 다익스트라와 똑같다.

 

결국 해당 문제는 어떻게 그래프 정보를 저장하고, 어떻게 다익스트라 문제로 유도할 수 있는가에 달려있다.

---

전체 코드이다.

public class Main {
    private static List<Path>[]list;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int n = Integer.parseInt(st.nextToken());
        int m = Integer.parseInt(st.nextToken());

        list = new List[360001];
        for(int i=0;i<=360000;i++)list[i] = new ArrayList<>();

        for(int i=1;i<=n;i++){
            String s = br.readLine();
            for(int j=1;j<=m;j++){
                if(s.charAt(j-1) == '/'){
                    addEdge(hash(i-1, j), hash(i, j-1), 0);
                    addEdge(hash(i-1, j-1), hash(i, j), 1);
                }
                else{
                    addEdge(hash(i-1, j-1), hash(i, j), 0);
                    addEdge(hash(i-1, j), hash(i, j-1), 1);
                }
            }
        }

        int[]dist = new int[360001];
        Arrays.fill(dist, Integer.MAX_VALUE);
        PriorityQueue<Path>pq = new PriorityQueue<>();
        Path p = new Path(0, 0);
        pq.add(p);

        dist[0]= 0;
        while(!pq.isEmpty()){
            int cur = pq.peek().nxt;
            int cost = pq.peek().cost;
            //System.out.println("cur="+cur+" "+"cost="+cost);
            pq.remove();

            if(cost > dist[cur])continue;
            for(Path temp : list[cur]){
                if(dist[temp.nxt] > cost+temp.cost){
                    dist[temp.nxt] = cost+temp.cost;
                    Path t = new Path(temp.nxt, dist[temp.nxt]);
                    pq.add(t);
                }
            }
        }


        int ans = dist[hash(n+1, m+1)];
        if (ans != Integer.MAX_VALUE) {
            System.out.println(ans);
        } else {
            System.out.println("NO SOLUTION");
        }
    }
    private static int hash(int x, int y){
        return x*555+y;
    }
    private static void addEdge(int s, int e, int cost){
        Path p1 = new Path(e, cost);
        list[s].add(p1);

        Path p2 = new Path(s, cost);
        list[e].add(p2);
    }

}
class Path implements Comparable<Path>{
    int nxt;
    int cost;
    Path(int nxt, int cost){
        this.nxt = nxt;
        this.cost = cost;
    }

    @Override
    public int compareTo(Path p){
        return this.cost - p.cost;
    }
}