백준 6549 (히스토그램에서 가장 큰 직사각형) <세그먼트 트리>

문제

6549번: 히스토그램에서 가장 큰 직사각형

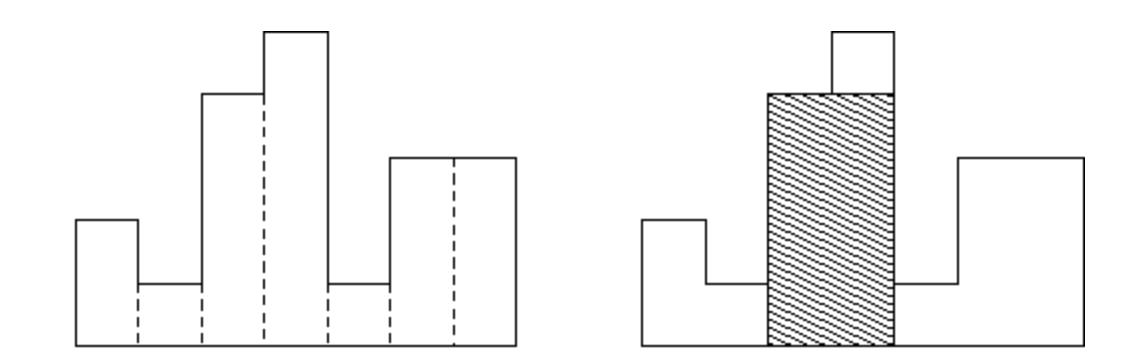
n개의 밑변의 길이가 1이고 높이가 다른 직사각형이 주어지면, 가장 큰 직사각형을 구하는 문제이다.

이전에 스택으로 푼 문제지만, 이번에는 세그먼트 트리를 이용해 문제를 풀어보겠다.

 

중요한 것은 0 ~ n-1 의 구간이 있으면, 구간을 돌아보면서 만들 수 있는 가장 큰 직사각형을 return 한다.

따라서 구간의 가장 큰 직사각형의 넓이는 구간 중 가장 작은 높이와 구간의 길이를 곱해주면 된다.

 

이를 위해 각 구간에서 가장 작은 높이를 가지고 있는 직사각형의 인덱스를 세그먼트 트리에 저장한다.

init(1, 0, n-1);

private static int init(int idx, int s, int e){
        if(s==e)return tree[idx] = s;

        int mid = (s+e)/2;

        int leftIdx = init(2*idx, s, mid);
        int rightIdx = init(2*idx+1, mid+1, e);

        return tree[idx] = arr[leftIdx] < arr[rightIdx] ? leftIdx : rightIdx;
    }

위의 코드는 세그먼트 트리를 초기화 하는 부분이다.

서로 길이를 비교해주며, 길이가 작은 인덱스를 return 해준다.

sol(0, n-1);

private static void sol(long left, long right){
        if(left>right)return;

        int idx = query(1, 0, n-1, (int)left, (int)right); //가장 작은 높이의 인덱스

        ans = Math.max(ans, arr[idx] * (right-left + 1));

        sol(left, idx-1);
        sol(idx+1, right);
    }
    
private static int query(int idx, int s ,int e, int l, int r){
        if(e<l || r < s)return Integer.MAX_VALUE;
        if(l <= s && e <= r)return tree[idx];

        int mid = (s+e) / 2;
        int leftIdx = query(2*idx, s, mid, l, r);
        int rightIdx = query(2*idx+1, mid+1, e, l, r);

        if(leftIdx == Integer.MAX_VALUE)return rightIdx; //에러 방지용
        else if(rightIdx==Integer.MAX_VALUE)return leftIdx; //에러 방지용
        else return arr[leftIdx] < arr[rightIdx] ? leftIdx : rightIdx;
    }

이제 0 ~ n-1 까지 구간을 보며 가장 작은 높이의 인덱스를 idx에 저장하고

높이를 구하고 ans에 저장한다.

예를 들어 0 ~ 6 까지 구간을 보면 가장 작은 높이의 인덱스는 1이다. (4도 있지만, 4여도 상관없다)

출처 : https://cocoon1787.tistory.com/314

인덱스 1을 기준으로 두부분으로 나눈것이다.

왼쪽 도형은 ans가 2로 left와 right가 같으므로 종료된다.

오른쪽 도형은 다시 2 ~ 6까지 중에 가장 작은 높이의 인덱스를 return 한다. 바로 4이다.

또 4를 기준으로 left, right를 나누고 계속 진행된다.

이런식으로 ans 값을 갱신하면 결국 최댓값이 나오게 된다.

---

전체 코드이다.

public class Main {
    private static int n;
    private static int[]arr;
    private static int[]tree;
    private static long ans;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        while(true){
            ans=0;
            st = new StringTokenizer(br.readLine());
            n = Integer.parseInt(st.nextToken());
            if(n==0)break;
            arr = new int[n];
            tree = new int[n*4];
            for(int i=0;i<n;i++)arr[i] = Integer.parseInt(st.nextToken());
            init(1, 0, n-1);
            sol(0, n-1);
            System.out.println(ans);
        }
    }
    private static int init(int idx, int s, int e){
        if(s==e)return tree[idx] = s;

        int mid = (s+e)/2;

        int leftIdx = init(2*idx, s, mid);
        int rightIdx = init(2*idx+1, mid+1, e);

        return tree[idx] = arr[leftIdx] < arr[rightIdx] ? leftIdx : rightIdx;
    }

    private static int query(int idx, int s ,int e, int l, int r){
        if(e<l || r < s)return Integer.MAX_VALUE;
        if(l <= s && e <= r)return tree[idx];

        int mid = (s+e) / 2;
        int leftIdx = query(2*idx, s, mid, l, r);
        int rightIdx = query(2*idx+1, mid+1, e, l, r);

        if(leftIdx == Integer.MAX_VALUE)return rightIdx;
        else if(rightIdx==Integer.MAX_VALUE)return leftIdx;
        else return arr[leftIdx] < arr[rightIdx] ? leftIdx : rightIdx;
    }

    private static void sol(long left, long right){
        if(left>right)return;

        int idx = query(1, 0, n-1, (int)left, (int)right);

        ans = Math.max(ans, arr[idx] * (right-left + 1));

        sol(left, idx-1);
        sol(idx+1, right);
    }

}