Normalization

Features of Good Relational Design

instructor 와 department를 in_dep 라는 table로 합쳤다고 가정하면

같은 dept_name 정보가 반복해서 들어가고 중복이 발생합니다.

또는 새로운 학과가 만들어질 경우 교수가 아직 없다면 null 값으로 넣어 추가해야하는 문제도

발생합니다. 

따라서 무조건 table을 합친다고 좋은것이 아닙니다.

Decomposition (table 쪼개기)

위에서 본 문제를 해결하려면 in_dep relation을 두개로 쪼개야 합니다. (instructor과 department)

하지만 모든 decomposition이 좋은것은 아닙니다.

employee(ID, name, street, city, salary)를 

employee1(ID, name)

employee2(name, street, city, salary) 로 쪼개게 되면

만약 동명이인이 있을 경우 join 할 때 문제가 발생하게 됩니다.

동명이인이 있으면 정보 일부가 날라가 원래의 table로 복원이 불가하게 되는데 이를 lossy decomposition

이라고 합니다. (데이터 양(tuple)은 증가하는데 information은 누락(less) 됩니다.)

R1과 R2로 쪼개면 Kim 이라는 동명이인이 존재합니다. 이를 natural join하게 되면

불필요한 정보가 추가적으로 insert 됩니다.

Lossless Decomposition

말대로 정보손실이 없는 decomposition입니다.

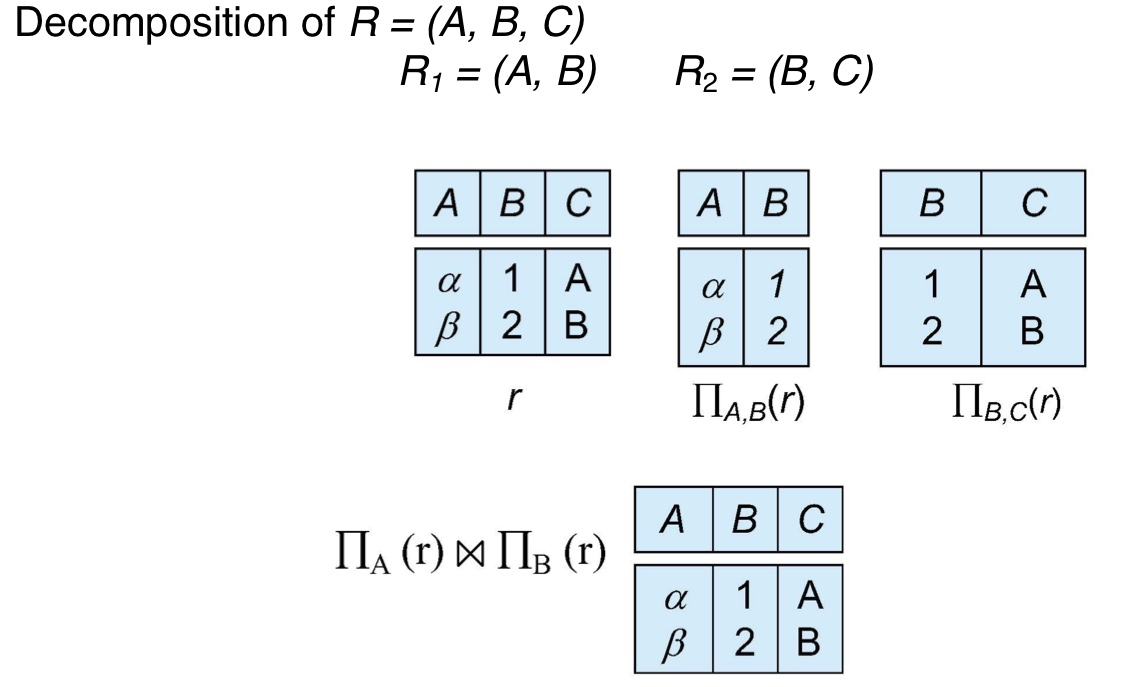
만약 R을 R1과 R2로 쪼개고 R 이 완전히 R1 ∪ R2를 만족한다면 R은 lossless decomposition입니다.

ex)

Normalization Theory

현재 relation R이 좋은 relation인지 decide하는 이론입니다.

만약 좋은 relation이 아니면 decompose(쪼개기) 해서 relation을 쪼개야 합니다. 

(쪼개진 relation은 good 형태여야 하고 , lossless decomposition이어야 합니다.)

크게 두개로 나누어 살펴보아야 합니다.

1. Functional dependencies

2. Multivalued dependencies

Functional Dependencies (함수 종속)

어떤 attribute X 의 값을 알면 다른 attribute Y의 값이 유일하게 정해지는 의존관계 입니다.

"attribute Y는 attribute X에 종속한다(dependent)" 혹은 "attribute X 는 attribute Y를 결정한다(determine)"

X → Y 로 표기하며, X를 Y의 결정자라고 합니다.

 

Determinant(결정자)

주어진 relation에서 다른 attribute 또는 attribute 들의 집합을 고유하게 결정하는 하나 이상의 attribute

다음과 같은 '수강' 이라는 relation이 있을 때 

학번을 알면 이름을 알 수 있습니다.

따라서 학번이 이름의 determinant가 되고 이름은 학번에 의해서 결정되며 이름이 학번에 종속됩니다.

학번과 교과명을 알게 되면 그에 따른 성적을 알 수 있습니다. 

따라서 학번과 교과명이 성적을 결정하는 determinant가 됩니다. 성적은 학번과 교과명에 종속됩니다.

determinant는 하나의 attribute가 될 수 도 있지만 여러개의 attribute로 이루어질 수 있습니다.

ex) 학번 → 이름

     {학번, 과목명} → 성적

 

functional dependecy a → b 는 a가 결정됨에 따라 b가 결정될 때에 어떤 legal relation r(R)에 대해서 

hold on R이 됩니다.

즉, 앞의 것이 UNIQUE 할때 뒤의 것이 하나로 결정되는 경우를 functional dependency가 hold 된다고 말합니다.

ex) A     B

     1     4

     1     5

     3     7

이라고 하면  B → A는 hold 이고  A → B는 hold가 아닙니다. 

Closure of a set of Functional Dependencies

만약 A → B이고 B → C라면 A → C 도 hold 입니다.

이렇게 fuctional dependencies의 집합 F가 주어졌을 때, F로부터 추론해서 얻어 낼 수 있는 

모든 fuctional dependency를 closure of F라고 부릅니다.

이는 F+라고 표기합니다.

Keys and Functional Dependency

K가 relation R의 superkey라고 하면 K → R 입니다. (반대도 성립)

K가 cadidate key라면

1. K → R 

2. a ⊂ K, a → R 인 또 다른 a는 존재하지 않습니다.

functional dependency는 우리가 superkey로는 표현하지 못했던 constraints를 표현할 수 있습니다.

ex) in_dep(ID, name, salary, dept_name, building, budget)

여기서 우리는 dept_name → building 또는 ID → building을 hold 할 수 있습니다.

하지만 dept_name → salary는 hold 하지 못합니다.

Use of Functional Dependencies

우리는 functional dependency를 사용합니다.

1. 주어진 functional dependencies에서 relation이 legal 한지 확인 하기 위해 사용합니다.

만약 functional dependencies F 에서, relation r이 legal 한다면 r satisfies F 라고 말합니다.

 

2. legal relation의 집합에서 constraints를 지정하기 위해 사용합니다.

만약 R의 모든 legal relation이 functional dependencies F를 만족한다면 F holds on R 이라고 합니다.

 

satisfy는 특정 instance가 functional dependency를 만족하는 것, hold는 schema 자체가 legal한 것입니다.

hold 하지 않더라도 우연히 satisfy는 할 수 있습니다.

예를 들어 어느 특정한 instace는 name → ID를 만족 할 수 도 있습니다.

Trivial(당연한 것) Functional Dependencies

A → A 또는 AB → A 같은 유형의 Functional Dependency은 모든 relation에 의해 satisfy 될때 trivial이라고 합니다.

ex)

name → name

ID, name → ID

일반적으로 만약 B ⊆ A 이면 A → B는 trivial 입니다.

 

Lossless Decomposition

functional dependency를 이용해 decomposition이 lossless 한지 아닌지를 검사할 수 있습니다.

예를 들어 R = (R1, R2) 라 하면 R을 R1과 R2로 decomposition할 때, 다음과 같은 종속성을 적어도 하나 F+가

가지고 있어야 lossless decomposition이라고 할 수 있습니다.

1. R1 ∩ R2 → R1

2. R1 ∩ R2 → R2

위의 functional dependency는 lossless join decomposition을 위해 필요한 조건입니다.

위 dependency는 모든 constraints가 functional dependencies인 경우에만 필요한 조건입니다.

 

좀더 공부하기 (보류)

 

Dependency Preservation

데이터 베이스가 업데이트 될때 마다 functional dependency constraints를 테스트하려면 비용이 많이 듭니다.

따라서 constraints를 효율적으로 테스트 할 수 있게 데이터베이스를 설계하는 것이 좋습니다.

하나의 relation만 고려해 functional dependency constraints를 테스트 할 수 있다면 비용이 적게 듭니다.

하지만 decomposition 과정에서 Cartesian Produced을 사용하지 않으면 테스트 할 수 없게 되기도 합니다.

 

functional dependency를 확인하기 위해 join을 해야하는 등, 어렵게 만드는 decomposition의 경우, 

Not dependency preserving이라고 부릅니다.

 

ex) dept_advisor(s_ID, i_ID, dept_name)

여기서 functional dependency는 i_ID → dept_name 와 s_ID, dept_name → i_ID 입니다.

이 경우 instructor가 dept_advisor relation에 참여할 때 마다 department_name을 계속해서 반복해서 적어줘야

합니다.

이러한 중복성을 해결하기 위해 decomposition을 해줘야 하는데, 이 경우 어떻게 나눠도 s_ID, dept_name → i_ID

를 포함할 수 없으므로 이 decompositon은 not dependency preserving 하다고 말할 수 있습니다.

 

Boyce-Codd Normal Form (BCNF)

a ⊆ R 그리고 b ⊆ R 일때 a → b를 만족한다고 가정하면

1. a → b 가 trivial하다. (b ⊆ a)

2. a가 R의 superkey이다.

F+의 모든 functional dependencies가 위의 조건중 최소 1개를 만족하면 relation R이 BCNF를 만족한다고

할 수 있습니다.

 

ex) in_dep(ID, name, salary, dept_name, buliding, budget) 가 있다고 가정하면

dept_name → building, budget 이라는 functional dependency가 있을 경우 hold를 하긴하지만 dept_name이 

superkey가 아니므로 BCNF가 아닙니다.

 

만약 Violation of BCNF가 일어날 경우, Decompose를 해줘야 합니다.

1. a ∪ b

2. R - (b - a)

위 2가지로 decompose 할 수 있습니다.

위의 예시를 다시 활용하면

in_dep(ID, name, salary, dept_name, buliding, budget) 여기에서 a = dept_name, b = building, budget

1, a ∪ b = (dept_name, building, budget)

2. R - (b - a) = (ID, name, dept_name, salary)

 

BCNF and Dependency Preservation

BCNF와 dependency preserving decomposition을 언제나 동시에 만족 시킬 수 없습니다.

ex) dept_advisor(s_ID, i_ID, department_name) 을 고려하면

R1(i_ID, dept_name), R2(s_ID, i_ID) 라고 하면

i_ID → dept_name

s_ID, dept_name → i_ID 가 있을 때

i_ID가 superkey가 아니므로 decomposition을 해야합니다.

근데 어떤 decomposition을 하더라고 s_ID, dept_name → i_ID의 모든 attribute를 포함하지 못합니다.

따라서 이 decomposition은 not dependency preserving입니다.

 

Third Normal Form

BCNF 보다 조금 더 완화된 형태의 normal form입니다.
relation R 이 있다고 하면
1. a → b 가 trivial (b ∈ a)
2. a가 R의 superkey 이다.
3. b-a에 있는 attribute가 R의 candidate key에 포함
위 3가지 조건중 1가지만 충족시키면 3NF 입니다.

BCNF 이면 3NF입니다. 반면에 3NF이면 BCNF 일 수 도 있고 아닐 수 도 있습니다.
ex) dept_advisor(s_ID, i_ID, dept_name)
function dependency :
i_ID → dept_name 
s_ID, dept_name → i_ID
두개의 candidate key는 {s_ID, dept_name}, {s_ID, i_ID} 입니다.

다시 보면 s_ID와 dept_name은 superkey 입니다. (2번 조건)
i_ID는 superkey는 아니지만, {dept_name} - {i_id} = {dept_name} 이고 dept_name은 cadidate key에 포함되므로
3NF는 만족합니다. (3번 조건)

 

Redundancy in 3NF

다음과 같은 R을 고려해봅시다.

1. 정보의 중복이 발생

2. NULL 값을 사용

 

Comparison of BCNF and 3NF

3NF는 언제나 lossless 하고 dependency preserving한 3NF design을 얻을 수 있습니다.

하지만 데이터 간의 의미있는 관계 중 일부를 나타내려면 null 값을 사용해야 하는데 이는 BCNF가 유리하고

또한 정보의 중복 문제도 BCNF가 더 유리합니다.

 

Goals of Normalization

R이 라는 relation schema와 F라는 Functional dependency가 있을 때 R이 좋은 relation인지 판별하고

아니라면 relation을 decompose합니다.{R1, R2, R3, ...Rn}

이 때 각 relation schema는 good 형태이어야 하며, lossless decomposition이어야 하고 dependency preserving

해야 합니다.

 

How good is BCNF?

BCNF이지만 충분히 normalized가 안된 relation을 고려해보자

inst_info(ID, child_name, phone)

instructor는 한개 이상의 phone을 가질 수 있고 여러명의 child를 가질 수 있습니다.

 

trivial fuctional dependency 이므로 BCNF에 해당한다고 불 수 있습니다.

위의 relation은 삽입 이상(insertion anomaly)이 발생했습니다.

*삽입 이상 : 불필요한 정보를 함께 저장하지 않고서는 어떤 정보를 저장하는 것이 불가능

만약 ID 99999에 phone 981-992-3443을 추가하려면 2개의 tuple을 추가해야 가능합니다.

(99999, David, 981-992-3443)

(99999, William, 981-992-3443)

 

따라서 inst_info를 2개로 decompose 하는 것이 좋아보입니다.

inst_child

inst_phone

이것은 4NF 라는 higer normal form을 요구합니다. 이는 나중에 살펴보겠습니다.

 

Closure of a Set of Functional Dependencies

Functional dependency의 집합 F로 부터 추론될 수 있는 모든 functional dependency를 closure라고 합니다.

만약 A → B 와 B → C 로 부터 A → C를 추론할 수 있습니다.

이는 F+로 표현할 수 있습니다.

 

우리는 Armstrong's Axioms 로 부터 F+를 계산할 수 있습니다.

1. Reflexive rule : b ⊆ a 이면 a → b

2. Augmentation rule : a → b 이면 xa → xb

3. Transitivity rule : a → b 그리고 b → x 이면 a → x

 

위의 법칙들은 다음의 2가지로 나뉘어 집니다.

Sound : generate only functional dependencies that actually hold

Complete : generate all functional dependencies that hold

 

ex) relation R = (A, B, C, G, H, I) 라고 하면

F = {A → B, A →C, CG → H, CG → I, B →H}

위의 F로 부터 다음과 같은 Functional dependency를 유추할 수 있습니다.

1. A → H

Transitivity rule 에 의해 A → B, B → H 이므로 A →H 입니다.

 

2. AG → I

Augmentation rule 에 의해 A → C는 AG → CG 가 되고 Transitivity rule 에 의해 AG →CG, CG → I 

이므로 AG → I 가 됩니다.

 

3. CG → HI

Augmentation rule에 의해 CG → CGI 를 유추할 수 있습니다.Augmentationa rule 에 의해 CG → H 를 통해

CGI → HI를 유추할 수 있습니다.Transivity rule 에 의해 CG → CGI, CGI → H 이므로 CG → HI 가 됩니다.

 

이외 에도 새로운 rule이 존재합니다.

Union rule : A → B이고 A → C 이면 A → BC 입니다.

Decomposition rule : A → BC 이면 A → B  그리고 A → C 입니다.

Pseudotransitivity rule : A → B 이고 rB → q 이면 Ar → q 입니다.

위의 rule은 armstrong's axiom에서 유추할 수 있습니다.

 

Closure of Attribute Sets

F에 포함된 A라는 Attirbute의 closure를 구하는 방식입니다.

ex) R = (A, B, C, G, H, I) 라고 하면

F = {A → B, A → C, CG → H, CG → I, B →H} 

여기서 AG의 Closure을 구하면

result라는 변수에 AG과 관계된것을 모두 넣어줍니다. (AG+를 구하는것)

1. result = AG (자기 자신)

2. result = ABCG (A → C 그리고 A → B)

3. result = ABCGH (CG → H 그리고 CG ⊆ AGBC)

4. result = ABCGHI (CG → I 그리고 CG ⊆ AGBCH)AG+ = ABCGHI

 

AG는 candidate key인가?

이를 확인하기 위해서는 2가지 방법이 있습니다.1. AG가 super key 인지 확인AG → R ==AG+ ⊇ R 입니다.

2. AG의 subset이 super key 인지 확인

A → R == A+ ⊇ R

G → R == G+ ⊇ R 

 

Uses of Attribute Closure

1. Testing for superkey

A가 superkey라면 A+는 R의 모든 Attribute를 가지고 있어야 합니다.

 

2. Testing functional dependencies

A → B가 hold 한지 확인하려면  B ⊇ A+를 만족하는지 확인해보면 됩니다. 

 

3. Provides an alternative way of Computing closure of F

r ⊇ R이 있을 때 closure r+를 찾고 S ⊆ r+ 에 대해 r → S를 output으로 내보냅니다.

 

Canonical Cover

relation schema에 functional dependency F가 있다고 가정하면,

사용자가 relation을 업데이트 할 때 마다 DB 시스템은 업데이트된 사항이

F의 모든 dependency를 충족하는지 확인해야 합니다.

만약 violate(위반) 한다면 업데이트는 roll back 되어야 합니다.

우리는 주어진 functional dependency set과 같은 closure을 가진, 더 단순화 된 functional dependency를 

검사함으로서 드는 비용을 줄일 수 있습니다.

이러한 단순화된 functional dependency를 canonical cover라고 부릅니다.

 

Extraneous Attributes

없어도 상관없는 functinal dependency의 attribute입니다.

extraneous attribute를 다 지워야 canonical cover를 찾을 수 있습니다.

2가지 유형이 있습니다.

 

1. remove left side (stronger)

예를 들어 AB → C에서 A → C로 줄이면 강력해집니다.

왜냐하면 A → C는 AB → C를 추출할 수 있지만 AB → C는 A → C 를 추출할 수 없기 때문입니다.

그러나 functional dependency의 F가 어떻게 되느냐에 따라 AB → C에서 B를 안전하게 제거할 수 있습니다.

예를 들어 F = {AB → C, A →D, D → C} 라면 논리적으로 A → C를 추출가능하고 AB → C에서 B를 

extraneous로 만들 수 있습니다.

 

2. remove right side (weaker)예를 들어 AB → CD에서 C를 제거(AB → D)한다면 약해집니다.왜냐하면 AB → D에서 더이상 AB → C를 추출할 수 없기 때문입니다.그러나 functional dependency의 F가 어떻게 되느냐에 따라 AB → CD에서 C를 안전하게 제거할 수 있습니다.예를 들어 F = {AB → CD, A → C} 라면 AB → CD를 AB → D로 대체한 후에도 AB → C를 추출할 수 있고 따라서 AB → CD를 추출 가능합니다.

 

만약 F+를 변경하지 않고 제거할 수 있다면, F의 functional dependency의 attribute는 extraneous입니다.

F = {a → b} 라고 한다면

Remove from the left side

만약 A ∈ a 이고

F 가 논리적으로 (F - {a → b}) ∪ {(a - A) → b}를 추론할 수 있을 경우 A는 extraneous 합니다.

 

Remove from the right side

만약 A ∈ b 이고

F 가 논리적으로 (F - {a → b}) ∪ {(a → (b - A)}를 추론할 수 있을 경우 B는 extraneous 합니다.

 

Note : stronger functional dependency는 항상 weaker functinal dependency를 함축합니다.

 

Testing if an Attribute is Extraneous

F = {a → b}

1. A ∈ b일 때 extraneous 인지 아닌지 확인

F' = (F - {a → b}) ∪ {(a → (b - A)}F' 안의 a+가 A를 포함하는지 확인해보고 그렇다면 A는 extraneous 입니다.

 

2. A ∈ a 일 때 extraneous 인지 아닌지 확인

r = a - {A} 라고 하고  r → b 가 F로 부터 추출가능한지 체크합니다.r+를 계산해서 이게 b의 모든 attribute를 포함한다면, a에서 A는 extraneous 입니다.

 

EX) F = {AB → CD, A → E, E → C}AB → CD에서 C가 extraneous 인지 아닌지 확인해보자

먼저 C가 제거된 F' = {AB → D, A → E, E → C}에서 AB의 closure를 구하면

AB+ = ABCDE가 됩니다.ABCDE는 CD를 포함합니다.

따라서 C는 extraneous 입니다.

 

Canonical Cover

F의 canonical cover는 Fc입니다.F는 Fc에 있는 모든 dependency를 추론할 수 있습니다.

Fc는 F에 있는 모든 dependency를 추론할 수 있습니다.

Fc에는 extraneous attribute가 있으면 안됩니다.

Fc의 functional dependency의 왼쪽 side는 unique해야 합니다. (a1 → b1, a2 → b2 일 때 a1 = b1이면 안됩니다.)

 

canonical cover algorithm

1. F에 있는 dependency를 union rule을 활용해 a1 → b1, a1 → b2를 a1 → b1b2로 바꿉니다.

2. a → b에 있는 extraneous attribute를 없애줍니다.

3. 반복합니다. (Fc가 변경되지 않을 때 까지)

 

EX1) R = (A, B, C) , F = {A → BC, B → C, A → B, AB → C}

1. A →BC와 A → B를 A → BC로 결합합니다.

=> 그렇게 하면 F = {A → BC, B → C, AB → C}

 

2. A가 AB → C에서 extraneous인지 확인

A가 제거된 B → C가 유효한지 확인해야 합니다.

이미 F에 B → C가 있으므로 유효합니다.

=> 그렇게 하면 F = {A → BC, B → C}

 

3. C가 A → BC에서 extraneous인지 확인

C가 제거된 A → B나 다른 dependency에 의해 A → C를 추론할 수 있는지 체크해야합니다.

A → B, B → C를 통해 A → C 를 추론가능합니다.

 

따라서 canonical cover는 A → B, B → C 입니다.

 

EX2) R = (A, B, C, D), F = (A → BC, B → C, A → B, AB → C, AC → D}

1. A → BC와 A → B를 A → BC로 결합합니다.

=> 그렇게 하면 F = {A → BC, B → C, AB → C, AC → D}

 

2. A →BC에서 C가 extraneous attribute인지 확인

A+ = ABCD (C를 제거시켰음에도 불구하고 A의 close에는 C가 포함되기 때문에 C는 extraneous입니다.)

=> 그렇게 하면 F = {A → B, B → C, AB → C, AC → D} 

 

3. AB → C에서 C가 extraneous attribute인지 확인

AB+ = ABCD 이기 때문에 C가 포함됩니다.

따라서 C는 extraneous attribute이고 AB → C는 아예 삭제 됩니다.

=> 그렇게 하면 F = {A → B, B → C, AC → D}

 

4. AC → D에서 C가 extraneous attribute인지 확인 (left side 제거)

A+ = ABCD 이기 때문에 C는 extraneous 입니다.

=> 그렇게 하면 F = {A → B, B → C, A → D} 

=> Fc = {A → BD, B → C} 가 됩니다.

 

Dependency Preservation

R을 R1, R2, ,,,,Rn으로 decomposition 할 때 dependency a →  b가 preserving한지 확인하기 위해 

다음 알고리즘을 적용합니다.

a → b가 dependency preservation인지 확인하려고 합니다.

만약 result가 b의 모든 attribute를 포함한다면, functional dependency a → b는 preserving 한것입니다.

decomposition이 dependency preserving인지 확인하기 위해

우리는 위의 알고리즘을 F의 모든 dependency에 적용할 수 있습니다.

 

ex) R = (A, B, C), F = {A → B, B→ C}, Key = {A}

R은 BCNF가 아닙니다.

Decomposition R1 = (A, B), R2 = (B, C) R1과 R2는 BCNF 입니다. (A → C 는 자동적으로 확인)

따라서 해당 Decomposition은 Lossless-join decomposition 입니다.

Dependency preserving 합니다. 

 

Testing for BCNF

non-trivial dependency인 a → b가 BCNF의 violation을 일으키는지 확인하기 위해 아래 2가지를 체크합니다.1. a+ 계산2. 이러한 a+가 R의 모든 attribute를 포함하는지, 즉 R의 superkey인지 확인합니다.

 

만약 a가 superkey라면 BCNF를 만족하는것입니다.

 

Testing Decomposition for BCNF

R의 decomposition인 Ri가 BCNF인지 아닌지 체크하기 위해 몇가지의 테스트가 필요합니다.

a ⊆ Ri 라고 한다면 a+는 (Ri - a)의 어떠한 attribute도 포함하지 않거나(a가 functional dependency에 존재하지 않는 경우) 또는 Ri의 모든 attribute를 포함한다면(a가 superkey 인 경우) Ri는 BCNF를 만족합니다.

 

만약 위의 조건을 위반한다면 a → (a+ - a) ∩ Ri를 만족하게 되고 결국 Ri는 BCNF가 아니게 됩니다.

 

EX) R2 = (A, C, D, E) , F = {A → B, BC → D}

a = {A, C} ⊆ R2, (AC)+ = {ABCD} 는 (Ri - a) = {D, E} 를 통해 D를 포함합니다.

AC → (({ABCD} - {AC}) = {BD} ∩ R2) = {D}) 가 되고 즉 AC → D 가 됩니다.

R2 = (A, C, D, E) 가 R3 = {A, C, D}, R4 = {A, C, E}로 decomposition 됩니다.

R3와 R4는 BCNF 입니다.

 

BCNF Decomposition Algorithm

R = (A, B, C, D, E) , F = {A → B, BC → D}

위의 알고리즘을 모두 수행하면 각 Ri들은 모두 BCNF이고 lossless-join 입니다.

 

EX) class(course_id, title, dept_name, credits, sec_id, semester, year, building, room_number, capacity, time_slot_id)

F = {course_id → title, dept_name, credits

       building, room_number → capacity

       course_id, sec_id, semester, year → building, room_number, time_slot_id}

candidate key = {course_id, sec_id, semester, year}

 

이제 BCNF decomposition을 하겠습니다.

course_id → title, dept_name, credits는 만족하지만 course_id는 superkey가 아닙니다.

따라서

course(course_id, title, dept_name, credits)

class-1(course_id, sec_id, semester, year, building, room_number, capacity, time_slot_id) 으로 decomposition

 

course는 BCNF 입니다.

building, room_number → capacity는 class-1을 만족하지만  {building, room_number}는 class-1의 superkey가 아닙니다.우리는 class-1을 다시 decomposition할 수 있습니다.

classroom(building, room_number, capacity)section(course_id, sec_id, semester, year, building, room_number, time_slot_id)

 

classroom과 section는 BCNF 입니다.

 

Third Normal Form

BCNF는 dependency preserving을 유지하지 못합니다. functional dependency를 update할 때마다 체크하는 것은 중요합니다.따라서 BCNF보다 약한 normal form인 3NF를 사용합니다.

 

• 조금의 중복을 허용
• 각각의 relation에서 join없이 functional dependency를 체크
• 항상 lossless-join, dependency preserving decomposition

EX)

dept_advisor(s_ID, i_ID, dept_name)

F = {s_ID, dept_name → i_ID, i_ID → dept_name}

2개의 candidate key = {s_ID, dept_name}, {i_ID, s_ID}

 

R은 3NF

s_ID, dept_name → i_ID

(s_ID, dept_name)은 superkey

 

i_ID → dept_name

dept_name은 candidate key에 포함

 

Testing for 3NF

F+에 있는 모든 functional dependency를 체크할 필요가 없고 F에 있는 functional dependency만 체크해 주면

됩니다.

a → b에서 a가 superkey 이면 attibute closure를 사용해 a → b의 각 dependency를 체크

a가 superkey가 아니면 b의 각 attribute가 R의 candidate key에 포함되는지 안되는지 체크해줘야 합니다.

 

이러한 test는 expensive합니다.

따라서 3NF를 Testing하는 것은 NP-hard(그냥 어려움)합니다.

흥미롭게도 3NF를 decomposition하는 것은 polynomal time이 듭니다.

 

3NF Decomposition Algorithm

이러한 알고리즘을 통해 decomposition된 Ri 들은

3NF를 만족하고

dependency preserving과 lossless-join을 만족합니다.

 

EX)

cust_banker_branch = (customer_id, employee_id, branch_name, type)

F = {customer_id, employee_id  → branch_name, type,

        employee_id → branch_name,

        customer_id, branch_name → employee_id}

 

1번째 dependency에서 오른쪽에 있는 branch_name은 extraneous이기 때문에 제거합니다.

나머지 attribute에서는 extraneous가 없으므로 

Fc = {customer_id, employee_id → type,

          employee_id → branch_name,

          customer_id, branch_name → employee_id}

 

(custoemr_id, employee_id, type) = R1

(employee_id, branch_name) = R2

(cutomer_id, branch_name, employee_id) = R3

이제 3NF Decomposition 알고리즘을 적용하겠습니다.

 

먼저 R1은 원래 candidate key인 customer_id와 employee_id를 포함하므로 더이상 추가해줄것이 없습니다. 

R2 ⊆ R3이기 때문에 R2는 없어집니다.

결론적으로 

R1 과 R3만 남게 됩니다.

 

Comparison of BCNF and 3NF

둘다 decomposition이 lossless입니다.

하지만 3NF는 dependency가 perserved합니다.

BCNF는 dependency preserving이 보장되지는 않습니다.

 

Design Goals

relation database 을 설계하는데 목표는

BCNF, lossless join, dependency preservation을 만족시키는 것입니다.

만약 만족을 못한다면 dependency preservation을 포기하거나 BCNF를 포기해 3NF로 만족할 수 있습니다.

하지만 BCNF를 만족하는게 제일 좋기는 합니다.

이러한 목표들은 SQL에서는 고려하지 않기 때문에 설계할 때 미리 고려해줘야합니다.

 

Multivalued Depedencies (MVDs)

만약 우리가 instructor를 위해 children의 이름과 핸드폰 번호를 저장한다고 가정해봅니다.

inst_child(ID, child_name)

inst_phone(ID, phone_number)

만약 이러한 relation들을 합친다고 하면

inst_info(ID, child_name, phone_number)

 

ex)

(99999, David, 512-555-1234)

(99999, David, 512-555-4321)

(99999, William, 512-555-1234)

(99999, William, 512-555-4321)

이러한 relation은 BCNF입니다. 3개의 attribute 모두 포함되어야 superkey이므로 trivial 하기 때문입니다.

하지만 위의 table은 중복이 많이 일어납니다.

 

relatoin R을 3개의 null이 존재하지 않는 부분집합으로 분할된 attribute 집합을 가진 schema라고 가정해봅니다.

R = (Y, Z, W)

R의 모든 tuple(r)중에서 <y1, z1, w1> ∈ r 을 만족하고 <y1, z2, w2> ∈ r을 만족하면

<y1, z1, w2> ∈ r 과 <y1, z2, w2> ∈ r을 만족합니다. 

이를  Y →→ Z 라고 표시합니다.

Y→→W 가 만족하면 Y→→Z가  만족합니다.

 

다시 정리하면 relation R에서 a ⊆ R을 만족하고 b ⊆ R을 만족한다고 가정하면 multivalued dependency인 경우

a →→ b라고 씁니다. (a에 따라 b가 결정되지만 b가 multivalue인 경우)

이는 공식으로 정리되있습니다.

1) attribute가 a인 모든 tuple이 같아야 합니다. 

(가), (가), (가), (가)

 

2) attribute가 b인 3번째 tuple과  1번째 tuple이 같아야합니다.

(가,나1 , ), (가, , ), (가,나2 , ), (가, ,)

 

3) relation R의 모든 attribute중에서 b를 뺀[R - B] attribute중 3번째 tuple과 2번째 tuple이 같아야 합니다.

(가,나1, ), (가, ,다1), (가,나1, 다1), (가, ,) 

 

4) attibute가 b인 4번째 tuple과 2번째 tuple이 같아야 합니다.

(가, 나1, ), (가, 나2, 다1), (가, 나1, 다1), (가, 나2, )

 

5) relation R의 모든 attribute중에서 b를 뺀[R-B] attribute 중 4번째 tuple과 1번째 tuple이 같아야합니다.

(가, 나1, 다2), (가, 나2, 다1), (가, 나1, 다1), (가, 나2, 다2)

 

결국 attribute a를 제외한 모든 조합을 나타냅니다.

 

EX) 위에서 본 예시를 활용하면

ID →→ child_name

ID →→ phone_number

이라는 정의를 내릴 수 있습니다.

ID = Y는 child_name = Z 와 phone_number = W에 연관을 가지고 있습니다.

그리고 Z와 W는 서로 독립적입니다.

 

R(A, B, C)

A →→ B를 만족하려면

(a, b1, c1), (a, b2, c2), (a, b3, c3), (a, b1, c2), (a, b1, c3), (a, b2, c1), (a, b2, c3), (a, b3, c1), (a, b3, c2)

같은 조합이 나옵니다.

a    b1     c1

      b2     c2

      b3     c3

3 * 3 = 9개의 조합

 

Use of Multivalued Dependencies

multivalued dependency는 두 가지 방법으로 사용합니다.

1. relation에서 주어진 functional dependency, multivalued dependency 하에 legal한지 결정

2. legal relation 하에서 constraints를 지정합니다.

 

만약 relation r이 주어진 multivalued dependency를 만족하지 못하면 우리는 r에 다가 새로운 tuple을 더해

r' 를 만들 수 있습니다.

 

multivalued dependency의 정의에 따라 우리는 이러한 정의를 도출할 수 있습니다.

만약 a → b이면 a →→ b 이다.

즉 모든 functional dependency는 multivalued dependency입니다.

 

clousure D+는 D로 부터 도출가능한 모든 functional dependency와 multivalued dependency를 의미합니다.

 

Fourth Normal Form

4NF를 만족하기 위해서는 다음과 같은 조건중 1개만 만족하면 됩니다. (a ⊆ R, b ⊆ R)

1. a →→ b 를 trivial (b ⊆ a 또는 a ∪ b = R)

2. a가 R의 superkey

4NF이면 BCNF입니다.

4NF Decomposition 

R = (A, B, C, G, H, I)

F = { A →→ B

        B →→ HI

        CG →→ H}

현재 R은 4NF가 아닙니다. 왜냐하면 A→→B와  A는 R의 superkey가 아니기 때문입니다.

A+ = ABHI이므로 A는 superkey가 아닙니다.

따라서 R을 decomposition 해야합니다.

1) R1 = (A, B) 

A →→ B 이기 때문에 A는 superkey이므로 R1은 4NF입니다.

 

2) R2 = (A, C, G, H, I) 

R2는 4NF가 아니기 때문에 다시 R3와 R4로 decomposition해야 합니다.

 

3) R3 = (C, G, H)

CG → H이기 때문에 CG+ = CGH 이기떄문에 R3는 4NF입니다.

 

4) R4 = (A, C, G, I)

R4는 4NF가 아니기 때문에 다시 R5와 R6로 decomposition해야 합니다.

 

5) R5 = (A, I)

A →→ B 이고 B →→ HI 이기 떄문에 A →→ HI를 도출할 수 있습니다.

A →→ HI는 A →→ H와 A →→ I로 나눌 수 있기 떄문에

R5는 4NF 입니다.

 

6) R6 = (A, C, G)

A와 CG가 trivial하기 떄문에 R6는 4NF입니다.

(A ∪ CG = R)