Indexing

Basic Concepts

index는 데이터 검색을 빠르게 하기 위함입니다.

Search Key : file안에 있는 record를 찾기 위한 attribute 집합입니다.

index file : 아래와 같은 record들을 구성합니다.

일반적으로 index file은 일반적인 file보다 작습니다.

 

index는 크게 

Ordered index : search key들은 차례대로 정렬 

Hash index : search key들이 "bucket" 이라는 곳에 hash function에 의해 분배

 

Ordered Index

Clustering index(primary index)

primary key의 성격과 같습니다. search key가 그대로 순서대로 file을 가리킵니다.

clustering index는 일반적으로 primary key지만 100퍼센트 그런것은 아닙니다.

 

Secondary index

보통 clustering index가 아닌 것은 secondary index라고 합니다.

secondary index로는 각 record를 구분할 수 없습니다.

 

Index-sequential file

clustering index에 있는 search key로 index한 sequential file

위에 file을 보면 맨 왼쪽의 ID라는 attribute를 기준으로 search key를 형성하였습니다.

ID라는 search key를 기준으로 index = clustering index

 

Dense Index Files

ordered index는 dense index와 sparse index 두 가지가 있습니다.

dense index record는 file에 있는 모든 search key의 값을 가지고 있습니다.

그래서 dense index에서 index record는 search key값과 그 search key값을 가지고 잇는 

첫번째 데이터 record에 대한 포인터를 포함합니다.

여기서 ID가 32343인 index record를 찾는 다면 우선 index file에서 index entry중에 32343인것을 찾아가고

그 포인터를 찾아가면 32343의 값을 가지고 있는 record를 찾을 수 있습니다.

dense index는 clustering index라서 동일한 search key값으로 정렬되기 때문에 같은 search key값을

가지는 것들이 뭉쳐있는 것입니다.

 

위에 file을 보면 search key가 dept_name이고 데이터가 dept_name으로 정렬된 데이터 file입니다.

그리고 dense index라서 모든 dept_name이 index file에 놓여져 있습니다.

여기서 history학과의 record를 찾는 다면 dept_name에서 search key가 history인 학과를 찾고

그 포인터를 찾아가게 됩니다.

이 포인터가 가리키는 부분에 가면 history값을 가지는 첫번째 record를 만나고 여기서 포인터를 쫓아 내려갑니다.

 

Clustering vs Nonclustering Index

indexing은 record를 검색하는 데 매우 유용합니다.

하지만 indexing은 데이터가 변경되면서 overhead를 일으킵니다.

record가 삽입되거나 삭제될 때 relation에 있는 모든 index는 업데이트 되어야 합니다.

또는 record가 업데이트 될때, 업데이트된 attribute에 있는 index는 업데이트 되어야 합니다.

 

clustering index는 index가 primary index이기 때문에 데이터가 search key attribute로 정렬되어 있어

같은 값을 가진 record들이 뭉쳐있기 때문에 쫓아 내려가면서 데이터를 찾을 수 있습니다.

반면서 secondary index라면 똑같은 search key를 가지는 record들에 대한 포인터 목록을 

각각 따로 저장해야 합니다. 그렇게 되면 느립니다.

 

Sparse Index Files

sparse index는 일부 search key에 대한 index record만을 포함합니다.

따라서 오직 relation이 search key로 지정되어 있을 때 즉, index가 clustering index인 경우에만

사용할 수 있습니다.

예를 들어 ID가 45565를 찾는 다면 index file에서 45565보다 작거나 같은 index를 찾아

그 포인터가 가리키는 record에서 시작해서 원하는 record를 찾을 때 까지 포인터를 쫓아쫓아 내려가면 됩니다.

 

dense index와 비교해서 삽입과 삭제에서 적은 공간으로 유리합니다.

하지만 record를 찾는 속도는 느립니다.

 

Secondary Index

secondary index는 file의 순차적 정렬과 다른 정렬을 지정하는 search key를 가지는 index입니다.

다시말해 search key의 순서가 record 순서와 상관이 없습니다.

index record는 특정 search key값을 가지는 모든 실제 record의 포인터를 가지고 있는 bucket를 가리켜야 합니다.

secondary index는 모든 search key값과 search key값을 가지는 record에 대한 포인터를 가지는

index 엔트리로 된 dense index여야 합니다.

clustering index는 순차적으로 데이터 파일이 저장되어 있기 때문에 몇몇의 search key값만 저장해도 중간에 

있는 search key값을 찾는 것이 가능했습니다.

하지만 secondary index는 search key 값들 중에 몇개만 저장하면 일반적으로 파일 전체를 검색하지 않고서는

중간에 있는 값을 가지는 record를 찾을 수 없습니다.

위에서 보는 것과 같인 bucket은 데이터 파일의 포인터를 가지고 있습니다.

salary가 80000인 index를 보면 bucket에 두개의 포인터가 존재하는 것을 알 수 있습니다.

그리고 이 포인터를 각각 salary가 80000인 record들을 가리키고 있습니다.

 

Multilevel Index

primary index가 메모리보다 크기가 더 크면 access하는 비용이 많이 듭니다.

index file이 메인 메모리에 유지될 만큼 충분히 크기가 작다면 index 엔트리를 찾는 데 걸리는 검색시간은

짧습니다.

하지만 전체 index file이 메모리에 유지할 수 없을 만큼 크다면 필요할 때 마다 index block을 disk로부터 가져와야

하고 그 block에 없을 경우 다음 index file에서 index 엔트리를 찾기 위해 여러 disk block을 읽어야만 합니다.

이 경우 원하는 index 엔트리를 찾을 때 까지 비용이 많이 듭니다.

 

이러한 문제를 해결하기 위해 disk에 저장된 primary index를 순차 파일로 취급하고 그리고 그 primary index에 대해서

sparse index를 만드는 것입니다.

따라서 outer index를 primary index의 sparse index를 만들고 inner index를 데이터 파일의 primary index 파일로

만드는 것입니다.

만약 outer index 조차 너무 커서 메인 메모리에 맞지 않을 경우 index에 다른 레벨을 또 하나 만들어주면 됩니다.

다시 말해 outer index에 대해서 또 다른 sarse index를 만들어 주는것입니다.

 

multilevel index는 이러한 모습을 가지고 있습니다.

multilevel index에서 record의 위치를 찾기 위해서는 우선 outer index에서 이진탐색을 사용해 원하는 record보다

작거나 같은 search key중에 가장 큰 값을 가져옵니다.

이 때 record의 포인터는 inner block을 가리키게 됩니다.

이 포인터가 가리키는 block을 다시 스캔해서 원하는 record 보다 작거나 같은 검색 값 중에서 가장 큰 값을 가지는

record를 찾습니다.

이렇게 찾은 record의 포인터를 쫓아가면 찾고자 하는 record를 포함하는 block을 가리키게 됩니다.

따라서 원하는 데이터가 이 block에 있다는 것을 알게 됩니다.

다시 그 block에서 다시 탐색을 하면 원하는 record를 찾을 수 있습니다.

 

Index Update : Deletion

삭제한 record가 file 내에서 특정 search key값을 가진 유일한 record라면 search key 또한 index로 부터 삭제됩니다.

 

single-level index 엔트리 삭제

• Dense index

search key를 삭제하는 것은 search key가 가리키는 record 삭제하는 것과 같습니다. 즉, 둘다 삭제됩니다.

• Sparse index

search key의 엔트리가 index 내에 존재하면, 그 엔트리를 file내의 다음 search key 값으로 대체함으로써

삭제합니다.

만약 다음 search key값이 이미 index 엔트리에 존재한다면 그 엔트리는 대체되는 대신에 삭제됩니다.

만약 ID가 32343을 삭제하면 33456을 가리키게 됩니다.

 

Index Update : Insertion

single-level index 삽입

삽입할 record에 있는 search key를 사용해 탐색을 수행합니다.

• Dense index

만약 search key값이 index에 없으면 그것을 삽입합니다.

index는 순차적 file로서 관리됩니다. 

따라서 새로운 엔트리를 위한 공간이 더 필요합니다.

• Sparse index

index에 file각 block에 대한 엔트리를 저장하면, 새로운 block이 생성되지 않는 한 index가 변할 필요가 없습니다.

이 경우, 새로운 block에 나타나는 첫번째 search key값이 index에 삽입됩니다.

 

multilevel 삽입과 삭제

알고리즘은 single level 알고리즘의 단순한 확장입니다.

 

B+ Tree Index Files

indexed-sequential file의 문제점을 해결하기 위해 만들어졌습니다.

sequential file은 앞서 본듯이 insert와 delete를 하게 될때 많은 비용과 공간을 필요로 합니다.

반면에 B+ tree index를 사용했을 때 장점은 삽입 및 삭제가 발생하더라도 작은 로컬 변동만으로

전체 file을 자동으로 재구성 하게 됩니다.

따라서 성능 유지를 위해 전체 file을 재구성할 필요가 없습니다. 하지만 B+ tree도 아주 작은 단점이 존재합니다.

추가적인 삭제에 대한 overhead나 공간적인 overhead가 든다는 것입니다.

하지만 단점보다 장점의 이득이 더크기 때문에 B+ tree는 광범위하게 사용되고 있습니다.

B+ tree의 전체적인 구조입니다. B+ tree는 root node와 internal node, leaf node로 이루어져 있습니다.

그리고 B+ tree는 balanced tree입니다. 따라서 root node로 부터 leaf node로 가는 paht(경로)가 동일합니다.

root node와 internal node는 주로 sparse index 부분이 되고 leaf node부분은 데이터 file을 가리키는 dense index

부분이 됩니다.

 

B+ tree는 다음과 같은 특징을 만족합니다.

• root node로 부터 leaf node로 가는 path(경로)의 길이가 동일합니다.
• root node나 leaf node가 아닌 각 node들은 ceil(n/2) ~ n개의 children node를 가질 수 있습니다.
• leaf node의 경우 ceil((n-1) / 2) ~ n-1의 개수의 값을 가지게 됩니다.
• special case                                                                                                                                                                       1. root node가 leaf node가 아닌 경우 root node는 적어도 두개의 childeren node를 가집니다.                                       2. root가 leaf node인 경우, 다시말해 tree에 다른 node가 없을 경우에는 root는 0 ~ (n-1) 개수의 값을 가집니다.

여기서 말하는 n은 하나의 node에 있는 포인터의 개수를 말합니다.

 

B+ Tree Node Structure

여기서 Ki는 search key값을 의미하고 Pi는 non-leaf node일 경우 children node를 가리키는 포인터이고

leaf node일 경우에는 그 search key값을 가지는 record를 가리키는 포인터가 됩니다.

즉 P는 포인터이고 K는 search key값입니다.

 

search key들은 무작위로 저장되어 있지 않고 모두 순서화 되어있습니다.

K1 < K2 < K3 < .....< K(n-1)

 

Leaf Nodes in B+ Tree

포인터로 시작해서 포인터로 끝나과 사이에 search key값이 들어가 있는 구조를 이룹니다.

leaf node에서 i가 1 ~ n-1일 때 포인터 Pi는 file record를 가리키는데 그 file record는 search key값 Ki를 

가지고 있습니다.

Li와 Lj가 leaf node이고 i가 j보다 작다면 Li의 search key값들은 Lj의 search key값 보다 작거나 같아야 합니다.

그리고 마지막 포인터인 Pn은 search key 순으로 다음 leaf node를 가리키게 됩니다.

각 leaf node들은 search key를 기반으로 순서대로 놓여있고 leaf node들을 search key순으로 연결하기 위해

Pn을 사용합니다.

이러한 순서는 연속적으로 file을 처리할 때 능률 적일 수 있습니다.

 

Non-Leaf Nodes in B+ Trees

non-leaf node는 leaf node에 대한 multilevel sparse index를 이루고 있습니다.

n개의 포인터를 가지고 있는 non-leaf node를 살펴보면 Pi가 가리키는 subtree내에 모든 search key값은

Ki 보다 작아야 합니다.

Pi가 2 ~ n-1인 경우 Pi가 가리키는 subtree내의 모든 search key값은 K(i-1) 보다는 크거나 같고

Ki보다는 작거나 같은 값을 가져야 합니다.

non leaf node의 구조는 모든 포인터가 tree node에 대한 포인터를 가지고 있다는 것을 제외하고는

leaf node와 동일합니다.

non leaf node는 n개의 포인터를 가지게 되고 적어도 ceil(n/2) 개의 포인터를 가져야 하는 조건을 만족시켜야합니다.

 

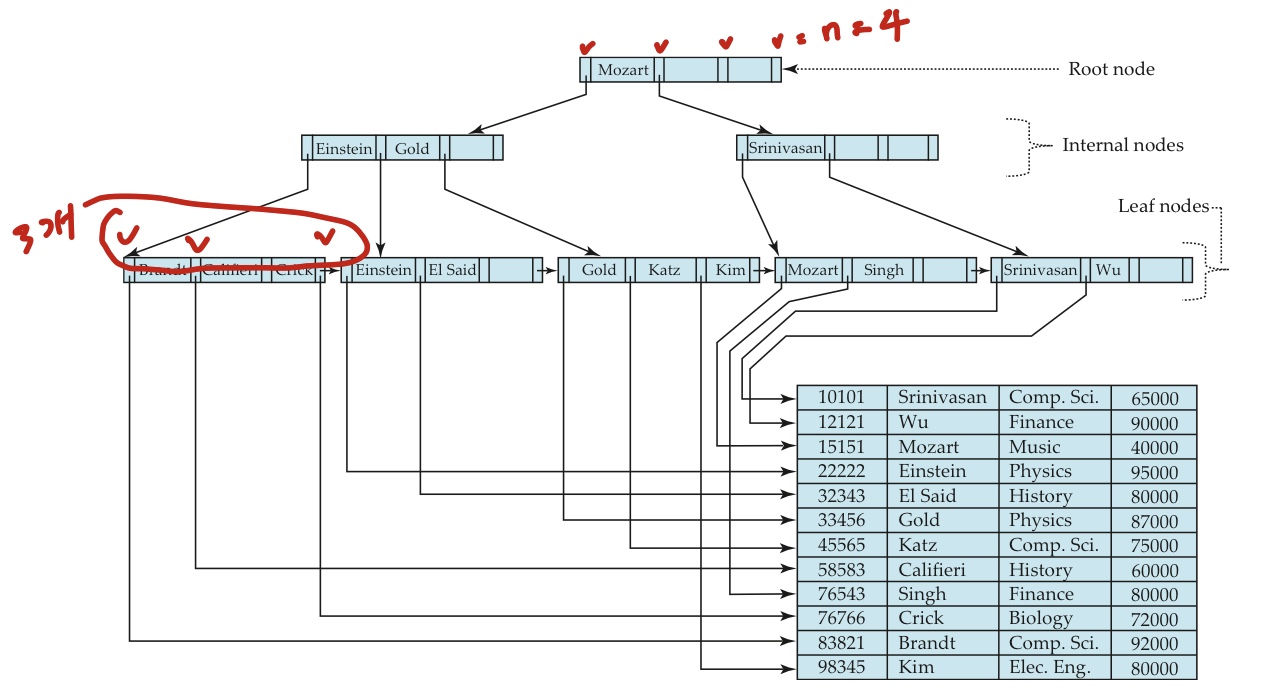
Example of B+ tree

1. n = 6 이기 때문에 leaf node들은 모두 3 ~ 5개의 search key값을 가져야 합니다.

2. root node가 아닌 non leaf node일 경우에는 3 ~ 6개의 childrent node를 가져야 합니다.

3. root node일 경우 적어도 2개의 children node를 가져야 합니다.

위에 B+ tree 예시를 보면 root node와 leaf node만 있으므로 두번째 조건은 확인하지 않아도 됩니다.

root node는 2개이상의 chlidren node를 가져야 하는데 3개의 포인터가 3개의 children node를 가리키고 있어

조건을 만족합니다.

leaf node도 3 ~ 5개 사이의 값을 가지고 있어 첫번째 조건을 만족하고 있습니다.

또한 root node의 첫번째 포인터가 가리키는 첫번째 node에 있는 search key값은 첫번째 search key값보다

작아야 하는데 Einstein이 El Said 보다 작기 때문에 조건을 만족하고 있습니다. (알파벳 순)

leaf node 마지막에 있는 포인터는 다음 leaf node를 가리킵니다. 연속적으로 file을 처리할 때 매우 효율적입니다.

 

Observations about B+ trees

internal node는 포인터로 이루어져 있어 B+ Tree는 논리적으로 근접한 block이 물리적으로 근접할 필요는 없습니다.

어떤 node가 바로 옆의 leaf node라고 해서 물리적으로 바로 옆에 있을 필요는 없습니다.

disk에 저장될 때 다른 부분에 저장될 수 있습니다.

B+ Tree의 leaf node가 아닌 계층들은 sparse index 계층을 이루게 됩니다.

B+ Tree는 비교적 적은 수의 계층을 가지고 있습니다. root의 children node에 저장할 수 있는 search key값들의 

개수는 적어도 2 * ceil(n/2)개 입니다.

다음 level은 2 * ceil(n/2) * ceil(n/2) 만큼 저장할 수 있습니다. 한 계층에 저장할 수 있는 search key값의 개수가 

많기 때문에 계층의 수가 작아질 수 있습니다.

따라서 file내 K개의 search key값이 있으면 tree의 높이는 ceil(log ceil(n/2) K) 보다 크지 않습니다.

그래서 검색이 효율적으로 이루어집니다.

file에서의 삽입과 삭제는 index가 log시간 내에 재구성이 될 수 있으므로 효과적으로 처리할 수 있습니다.

index는 데이터에 새로운 데이터가 추가되거나 기존의 데이터가 수정이나 삭제가 일어나면

index 자신도 갱신하는 기능을 가지고 있습니다.

갱신할 때마다 index 갱신도 부가적으로 발생하는데 이런것도 overhead의 일종입니다.

따라서 반드시 index를 많이 가지고 있다고 해서 효과적으로 데이터베이스를 사용할 수 있는것은 아닙니다.

 

Queries on B+ Trees

search key값이 v인 record인 것을 찾는 것입니다. find(v)

bianry search 와 같은 방식으로 구현됩니다.

 

ex) El Said라는 이름의 데이터를 찾는 다고 가정

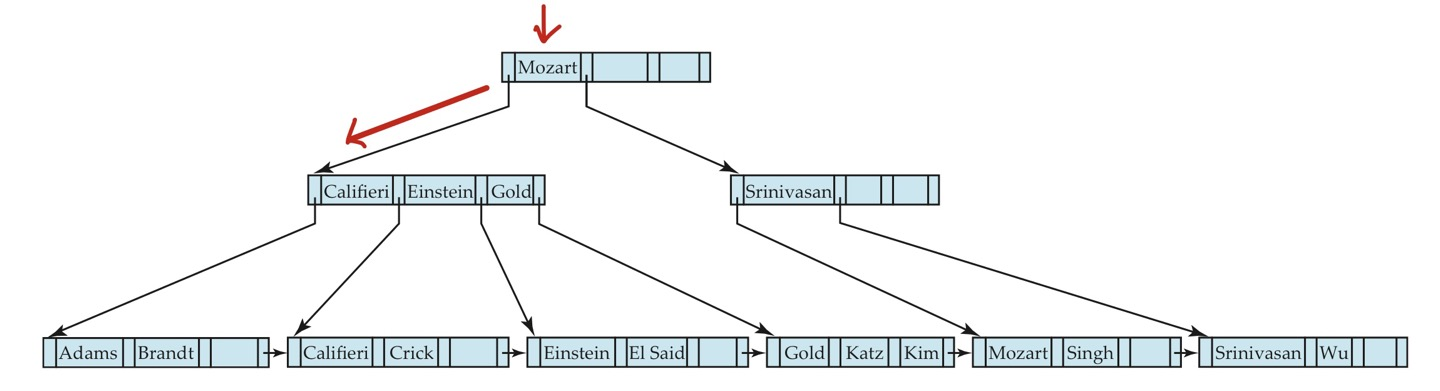
먼저 root node에서 첫번째 key 값부터 살펴보면 El Said보다 크거나 같은 최조의 key값을 찾습니다.

위의 그림을 보면 K0인 Mozart가 El Said보다 알파벳 순으로 크기 때문에 P0을 따라 다음 노드로 이동합니다.

다시 leaf node가 아니므로 K0부터 살펴보면서 El Said보다 크거나 같은 최최의 key값을 찾습니다.

위의 그림을 보면 K2인 Gold가 El Said보다 알파벳 순으로 크기 때문에 P2를 따라 다음 노드로 이동합니다.

이제 leaf node이므로 K0부터 살펴보면서 El Said를 찾습ㄴ디ㅏ.

위의 그림에서 K1이 El Said이므로 P1을 통해 데이터베이스에 접근해 우리가 찾는 데이터를 가져올 수 있습니다.

 

file내에 K개의 search key값이 있으면, tree의 높이는 ceil(log ceil(n/2)K) 보다는 크지 않습니다.

node는 일반적으로 disk block과 같은 크기인 4KB(4000 byte) 이며, n은 100정도입니다. (index 엔트리당 40 byte)

 

100만개의 search key값이 있고 n = 100인 경우

최대 log(50) 1000000 = 4개의 node가 탐색에서 access 됩니다.

 

이것을 100만개의 search key값을 가진 균형 이진 트리와 비교해보면 대략 20개의 node가 탐색에서 access 됩니다.

각 node의 access에는 대략 20ms가 걸리는 disk I/O 가 필요하게 되므로, 위와 같은 차이는 중요한 의미를 갖습니다.

 

Updates on B+ Trees : Insertion

삽입하는 과정은 다음과 같습니다.

 

먼저 삽입하려는 data의 key값과 일치하는 key값이 있는지 B+ tree index에서 찾습니다.

1. key값이 존재하면, 저장된 pointer를 통해 데이터베이스에 접근하여 데이터를 수정합니다.

2. key값이 존재하지 않으면

    2-1. 데이터베이스에 데이터 삽입

    2-2. B+ Tree의 leaf node(맨 처음 탐색한 위치)에 삽입할 공간이 있으면 삽입할 data의 pointer와 key값 삽입

    2-3. leaf node에 공간이 없으면 해당 node를 split(분할)후 빈 공간에 삽입합니다.

split이란 기존 node가 새로 삽입할 node를 포함해 n개의 (k, p) 쌍을 갖고 있다고 가정했을 때,

처음 ceil(n/2)개를 원래 node에 넣고, 나머지를 새로운 node에 넣습니다.

새로운 node를 p라고 하고, k를 p내의 가장 작은 key값이라고 하면 (k, p)를 분할 되고 있는 node의 부모에

삽입한다.

부모 node가 꽉 차면, 그것을 split하고 위로 계속 split해 나갑니다.

node의 split은 꽉 차지 않은 node가 발견될 때 까지 위로 진행해나갑니다.

최악의 경우에는 tree의 높이를 하나 더 증가 시키면서 root node가 분할 될 수 도 있습니다.

 

ex) Adams 라는 key값이 삽입되는 경우를 살펴봅니다. (n = 4)

먼저 Adams라는 key값을 탐색해보고, leaf node에 해당하는 key값이 존재하지 않는 것을 확인합니다.

이제 해당 leaf node에 새 (p, k)쌍을 삽입해야하는 데 공간이 없습니다.

따라서 해당 node를 split 해주어야 합니다.

기존 node의 쌍 3개 + 새로 삽입할 node의 쌍 1개 = 4개 이므로 뒤쪽 2개의 쌍을 떼어 새 node를 만들었습니다.

이 경우, Califieri와 Crick이 떼어져 새 node로 분리되었습니다.

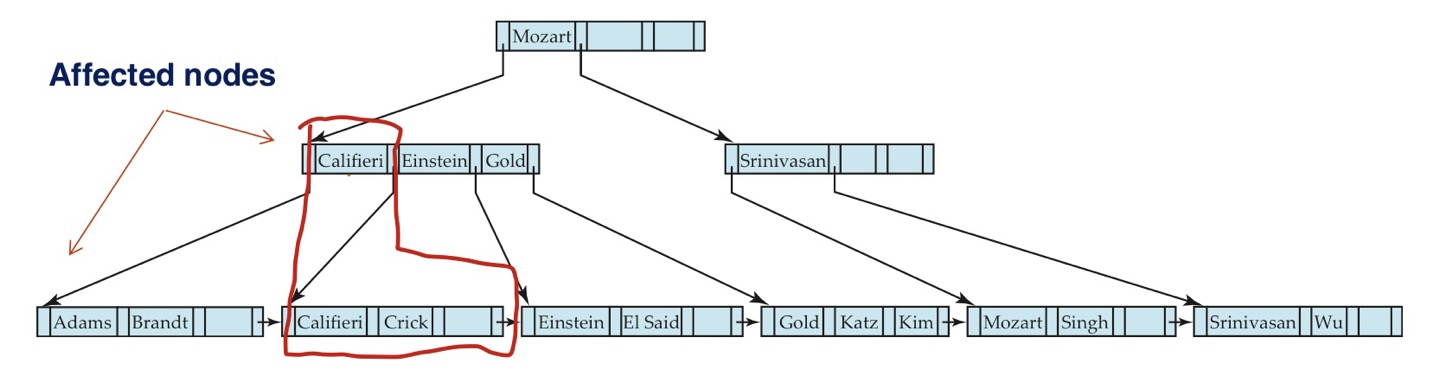
마지막으로 새로운 node가 추가되었으니 parent node에도 새 쌍을 추가해줍니다.

새 쌍을 추가한 parent node는 공간이 여유가 있으므로 split을 하지 않고 넣어주기만 하면 됩니다.

만약에 parent node에도 새깡을 추가할 공간이 부족하다면 parent node도 split 해주어야 합니다.

 

non-leaf node의 split : 이미 꽉 찬 internal node N에 (k, p)를 삽입하려고 하는 경우

1. n+1 개의 포인터과 n개의 key값을 갖는 메모리 영역 M에 N을 복사

2. (k, p)를 M에 삽입

3. M으로 부터 P1, K1, P2, K2, ....,K ceil(n+1/2)-1,P ceil(n+1/2) 을 N node에 복사

4. M으로 부터 P ceil(n+1/2)+1, K ceil(n+1/2) + 1, ...Kn, Pn+1을 새로이 할당받은 node N' 에 복사

5. (K ceil(n+1/2), N' )을 N의 node에 삽입

ex) Lamport라는 key값이 삽입되는 경우 (n = 4)

삽입전

삽입후

B+ Tree Deletion

1. B+ Tree index에서 key값을 검색하여 데이터의 위치를 찾아 데이터베이스에서 데이터를 삭제

2. B+ Tree index에서 삭제한 데이터의 (k, p)쌍을 삭제

3-1. 삭제 후 엔트리가 얼마 남지 않았고 형제 node와 merger가 가능한 경우 merge하여 하나의 node로 만듭니다.

3-2. 삭제 후 엔트리가 얼마 남지 않았지만, 형제 node와 merge가 불가능한 경우 redistribute합니다.

4. parent node에서도 (k, p)쌍을 삭제한 뒤 3-1과 3-2를 반복합니다.

 

이 때 , merge란 2개의 node를 합쳐 1개의 node를 만드는 작업이고

redistribute는 엔트리가 많은 node의 엔트리들을 엔트리가 적은 node로 옮겨 균형을 맞추는 작업입니다.

 

ex) Srinivasan 삭제

먼저 Srinivasan이라는 key값을 B+ Tree index의 leaf node에서 찾아 삭제합니다.

Srinvasan 엔트리를 삭제하자 Wu 엔트리 1개만 남게 되었고 이 때 형제 node에 공간이 남아있으니 merge합니다.

node를 merge하여 합치게 되니 parent node에 엔트리가 부족하게 되었습니다.

그러므로 형제 node의 엔트리 하나를 이동시켜 redistribute 해줍니다.

이제 엔트리가 부족한 node가 없으므로 deletion과정이 완료되었습니다.

 

ex) Singh과 Wu 삭제

leaf node에서 Singh와 Wu를 찾아 삭제하려고 하지만 해당 B+ Tree는 n = 4이므로 leaf node의 엔트리 개수는

최소 2개를 만족해야 합니다. 

따라서 Singh와 Wu를 모두 삭제하면 엔트리에 Mozart밖에 남지 않으므로 형제 node에서 하나의 엔트리를 

redistribute해야 합니다.

Kim을 오른쪽 node로 redistribute합니다.

다음과 같은 결과가 나옵니다.

 

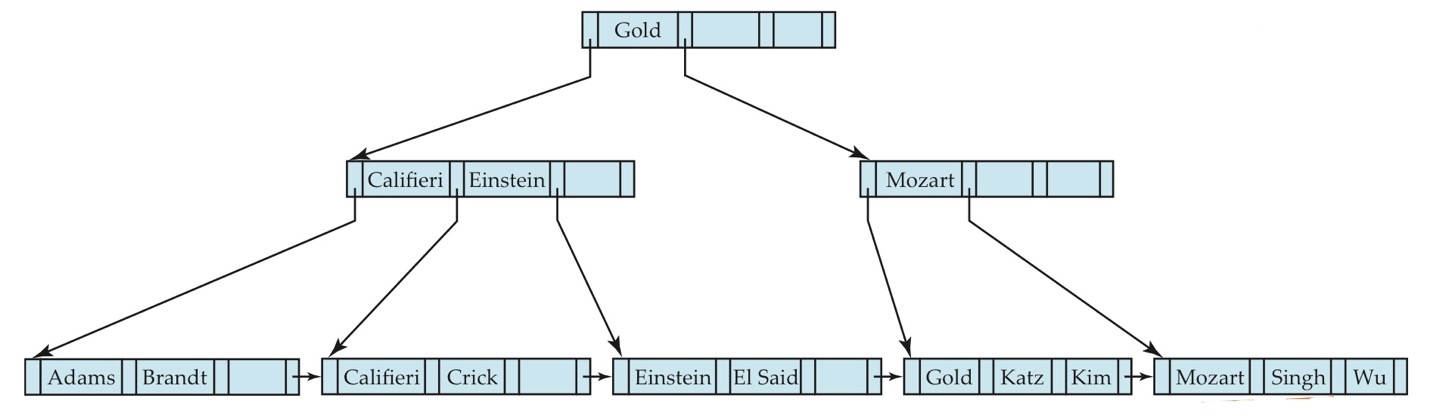
ex) Gold 삭제

위의 그림에서 Gold를 삭제하는 것입니다.

leaf node에서 Gold를 삭제하면 Katz만 남게 되므로 형제 node와 merge 해야합니다.

Kim, Mozart가 Katz쪽으로 merge하면 그 위의 parent node는 최소 엔트리를 유지하지 못해 삭제되므로

internal node는 1개만 남게 됩니다.

하지만 root node는 최소 2개이상의 internal node가 필요하므로 그냥 root node의 엔트리가 1개 남은 

internal node와 merge 하게 됩니다. (5-1)

따라서 root node의 Gold가 internal node로 들어오게 되면서 이에 대한 pointer도 같이 옵니다.(5-2)

위와 같이 됩니다. 

Gold가 삭제 됐지만 Gold가 맨 위의 node에 남아있는 것은 상관없습니다.

 

Complexity of Updates

insertion과 deletion의 비용은 

 

B+ Tree File Organization

index file의 성능 저하 문제는 B+ Tree index를 사용해 해결합니다.

data file의 성능 저하 문제는 B+Tree file organization을 사용해 해결합니다.

B+ Tree file organization의 leaf node에는 포인터 대신 record를 저장합니다.

leaf node에는 여전히 절반 이상이 차야합니다.

record는 포인터보다 크기 때문에, leaf node에 저장될 수 있는 record의 최대 수는 nonleaf node내 포인터의 

수보다 적습니다.

insertion과 deletion은 B+ Tree index 엔트리의 insertion, deletion과 같은 방법으로 처리됩니다.

위의 그림은 B+ Tree organization의 예시 입니다.

record는 포인터 보다 많은 공간을 사용하므로, 공간활용도가 중요합니다.

공간 활용도를 증가 시키려면, split 및 merge를 수행하는 동안 redistribution에서 더 많은 형제 node를 참여시킵니다.

redistribution에 2개의 형제 node를 참여시켜, 그 결과 각 node는 최소한 floor(2n/3)개의 엔트리를 갖게합니다.

 

Other Issues in Indexing

record가 이동하면, 해당 record에 대한 포인터 정보를 저장하고 있는 secondary index가 이에 따라 갱신되어야

합니다.

B+ tree file organization에서 node split에 따른 overhead가 매우 컵니다.

 

solution 

secondary index에서 record pointer 대신에 primary search key를 사용합니다. (salary, ID)

해당 record 검색을 위해 primary index를 부가적으로 탐색하여야합니다. (2번의 I/O 발생)

따라서 질의 처리를 위한 비용이 증가하지만, node split에 따른 overhead는 작아집니다. 

primary index key가 not unique하면 record-id값을 추가합니다.

 

B Tree Index Files

B+ Tree와 유사하지만, B Tree는 search key값이 단 한번만 나타나도록 하여 search key의 중복 저장을

제거합니다.

non leaf node 내 search key는 B Tree내 어디에도 나타나지 않습니다. 

non leaf node내 각 search key에 대해 추가의 포인터가 내포되어야합니다.(b)

일반적인 B Tree의 leaf node 구조입니다.(a)

 

non leaf node - 포인터 Bi 는 bucket 또는 file record 포인터입니다.

위는 B tree이고 아래는 B+ tree입니다.

둘다 똑같은 data입니다.

 

B Tree index의 장점

동등한 B+ Tree보다 적은 tree node를 사용합니다.

때로는 leaf node에 도달하기 전에 search key값을 찾을 수 있습니다.

 

B Tree index의 단점

모든 search key 값 중 극히 일부만이 조기에 찾을 수 있습니다.

non leaf node가 더 크므로, 전개(fan-out)이 감소합니다.

따라서 B Tree는 동등한 B+ Tree보다 일반적으로 높이가 더 높습니다.

B+ Tree 보다 insertion과 deletion이 더 복잡합니다.

B+ Tree보다 구현이 더 어렵습니다.

일반적으로 B Tree의 장점이 단점을 능가하지는 못합니다.