Chapter 3 : Arithmetic for Computers

Arithmetic for Computers

컴퓨터는 인간이 아니기 때문에 한정된 bit안에 수를 저장합니다.

만약 한정된 bit를 초과하는 수를 저장하면 Overflow가 발생합니다.

 

덧셈 연산에 overflow가 발생하는 경우는 다음과 같습니다.

1) 두 개의 양수를 더했는데 결과가 음수가 나옴

2) 두 개의 음수를 더했는데 결과가 양수가 나옴

 

뺄셈 연산에 overflow가 발생하는 경우는 다음과 같습니다.

1) 음수 - 양수의 결과값이 양수

2) 양수 - 음수의 결과 값이 음수

 

Dealing with Overflow

C언어의 경우 Overflow를 무시 

MIPS instruction에서는 add, addi, subu가 무시합니다.

 

반면에 다른언어(Ada, Fortan)의 경우 Overflow가 발생하게 되면 interrupt를 발생시킵니다.

MIPS instruction에서는 add, addi, sub가 interrupt발생시킵니다.

Overflow가 발생하면, exception handler를 호출합니다.

• PC(Program Counter)를 exception program counter(EPC) 레지스터에 저장합니다.
• 미리 정의된 handler의 주소로 점프합니다.
• mfc0 (coprocessor 레시스터로 부터 move) instruction은 수정 조치(corrective action)후에 return하기 위해            EPC의 값을 찾아낼 수 있습니다. (자세한건 Chapter 4)

Arithmetic for Multimedia (멀티미디어를 위한 산술)

Graphics와 media는 8-bit와 16-bit 데이터의 벡터 기반 작업을 수행합니다.

분할된 carry chain으로 작업합니다. 64-bit adder을 사용한다면, 총합이 64-bit 입니다.

(8 * 8 bit vector = 8개의 8bit 벡터를 한번에 연산), 2 * 32-bit, 4 * 16bit 에서 연산)

SIMD (Single-Instruction, Multiple-Data) : 하나의 insturction으로 여러개의 데이터 처리

 

Saturating operations

overflow가 발생한다면, 결과는 표현가능한 범위에서 가장 큰값이 됩니다. (넘치진 않고 MAX에서 멈춤)

c.f. 2's-complement modulo arithmetic

E.g., 오디오의 clipping, 비디오의 saturation(채도)

 

Multipilcation

곱셈

우리가 일반적으로 하는 곱셈방식과 유사합니다.

총 n bit라면 n번의 과정을 거칩니다.

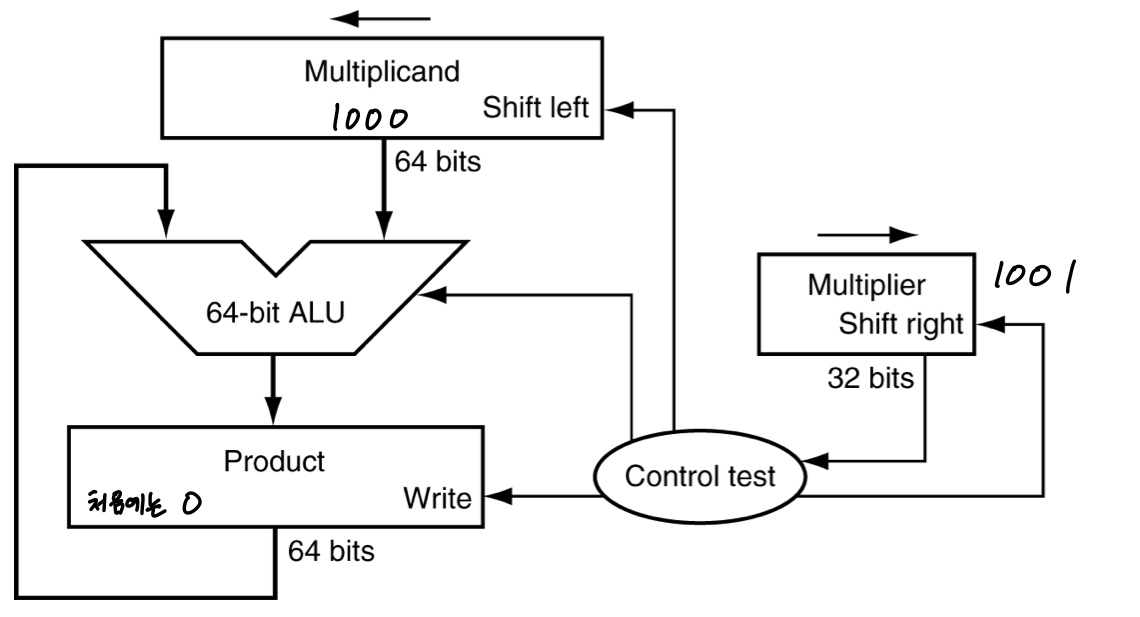
32 bit 두수를 곱에서의 실제 회로를 그림으로 나타낸것입니다.

여기서는 64 bit의 Multiplicand와 64 bit의 ALU가 필요합니다.

순서는 다음과 같습니다.

1) Multiplier의 맨 오른쪽 bit를 확인합니다.

2) bit가 1이면 multiplicand의 값을 Product에 더해줍니다. 반면에 bit가 0이면 더하지 않습니다.

3) 1, 2번을 마치고 Multiplier를 right shift합니다.

4) Multiplicand를 left shift합니다.

5) 1 ~ 4과정을 n번 반복 후의 Product값이 곱셈의 결과입니다.

위의 순서를 그림으로 나타내면 다음과 같습니다.

Optimized Multiplier

위의 과정을 하면 32 bit에서 64 bit ALU와 64 bit Multiplicand를 사용해야하는 불편을 감수해야합니다.

이를 개선한게 Optimized Multiplier입니다.

Optimized Multiplier는 32 bit의 ALU와 Multiplicand를 사용합니다.

Product의 왼쪽 32개의 bit는 덧셈을 위해 사용하고 오른쪽 32 bit는 Multiplier입니다.

먼저 Product 오른쪽에 있는 Multiplier 비트 중 맨 오른쪽의 bit를 확인합니다.

1이면 Product의 왼쪽 bit에 Multiplicand를 더하고 right shift합니다. 0이라면 그냥 right shift합니다.

위 과정을 n번 반복하면 Product의 bit를 통해 결과값을 확인할 수 있습니다.

 

ex) 0110(6) * 0101(5)

4 bit 두 수를 곱하는 예시입니다.

ALU와 multiplicand 모두 4 bit이고 product는 8 bit 입니다.

처음에 product 하위 4 bit는 multiplier로 채워진 채 시작합니다. (상위 4 bit = 0)

             Product          Multiplicand

1) 처음     0000                 0101

2) add      0110                 0101

3) shift     0011                 0010

4) add      0011                 0010 (맨 오른쪽 bit가 0이기 때문에 그대로 내려옵니다.)

5) shift     0001                 1001

6) add      0111                 1001

7) shift     0011                 1100

8) add      0011                 1100 (맨 오른쪽 bit가 0이기 떄문에 그대로 내려옵니다.)

9) shift     0001                 1110

4 bit 수의 곱이기 때문에 add/shift가 4단계 일어나면 종료합니다.

결과는 00011110 = 30

 

Faster Multiplier

위의 곱셈기는 32 bit 수의 곱이면 32번의 반복이 일어나게 됩니다.

이를 개선하고자 여러개의 adder를 사용합니다.

cost/performance 교환

결과를 빨리 얻을 수 있지만(성능은 높지만), 하드웨어를 많이 사용하므로 비용이 많이 듭니다.

pipeline화 가능합니다. 

각각의 곱 행동을 병렬적으로 으로 수행합니다. 이러면 적은 하드웨어 resource로도 빠른 연산이 가능합니다.

MIPS Multiplication

product에 2개의 32-bit 레지스터를 사용합니다. (결과는 64-bit로 저장되기 때문입니다.)

HI : most-significant 32 bits (상위 32 bit)

LO : least-significant 32 bits (하위 32 bit)

 

Instruction

mult re, rt   / multu rs, rt

HI와 LO로 64-bit의 product를 곱합니다. 

mfhi rd      /  mflo rd

HI/LO로부터 rd로 move

만약 product가 32 bit보다 커서 overflow가 될지 HI의 값을 미리 보려할 떄 사용할 수 있습니다.

mul rd, rs, rt

product의 하위 32 bit를 rd로

 

mult 나 multu가 64 bit 결과라면, mul은 32 bit 결과

 

Division

나눗셈

컴퓨터는 나눗셈을 뺄셈 연산을 통해 수행합니다.

예를 들어 5(dividend) / 2(divisor)

5에서 2를 뺍니다. 나머지의 값(3)이 2보다 큰지 확인합니다.

나머지가 2보다 크므로 다시 3에서 2를 뺍니다.

나머지의 값(1)이 2보다 작으므로 과정을 멈춥니다. 뺀 횟수가 몫이 되며 남은 값이 나머지가 됩니다.

컴퓨터에서 나눗셈은 뺄셈을 통해 수행되기때문에 0으로 나누는 일을 무한 루프가 발생할 수 있습니다.

나눗셈 연산에 이용되는 논리 회로입니다.

Remainder 레지스터에 dividend값이 들어있습니다. 

그리고 divisor의 왼쪽 bit에는 divisor의 값이 오른쪽에는 0으로 초기화 되어있습니다.

1) Remainder - Divisor 를 수행합니다.

2) 결과의 맨 왼쪽 bit를 확인합니다. 0이라면(양수) Quotient에 1을 put하고 left shift합니다.

3) 1(음수)이라면 Quotient에 0을 put하고 left shift한 후에 다시 Divisor를 더해 원래 값으로 back합니다.

4) Divisor을 right shift합니다.

5) 이 연산을 n번 반복하여 나온 remainder가 나머지가 되며 quotient에 저장된 bit의 맨 오른쪽 bit가 몫이 됩니다.

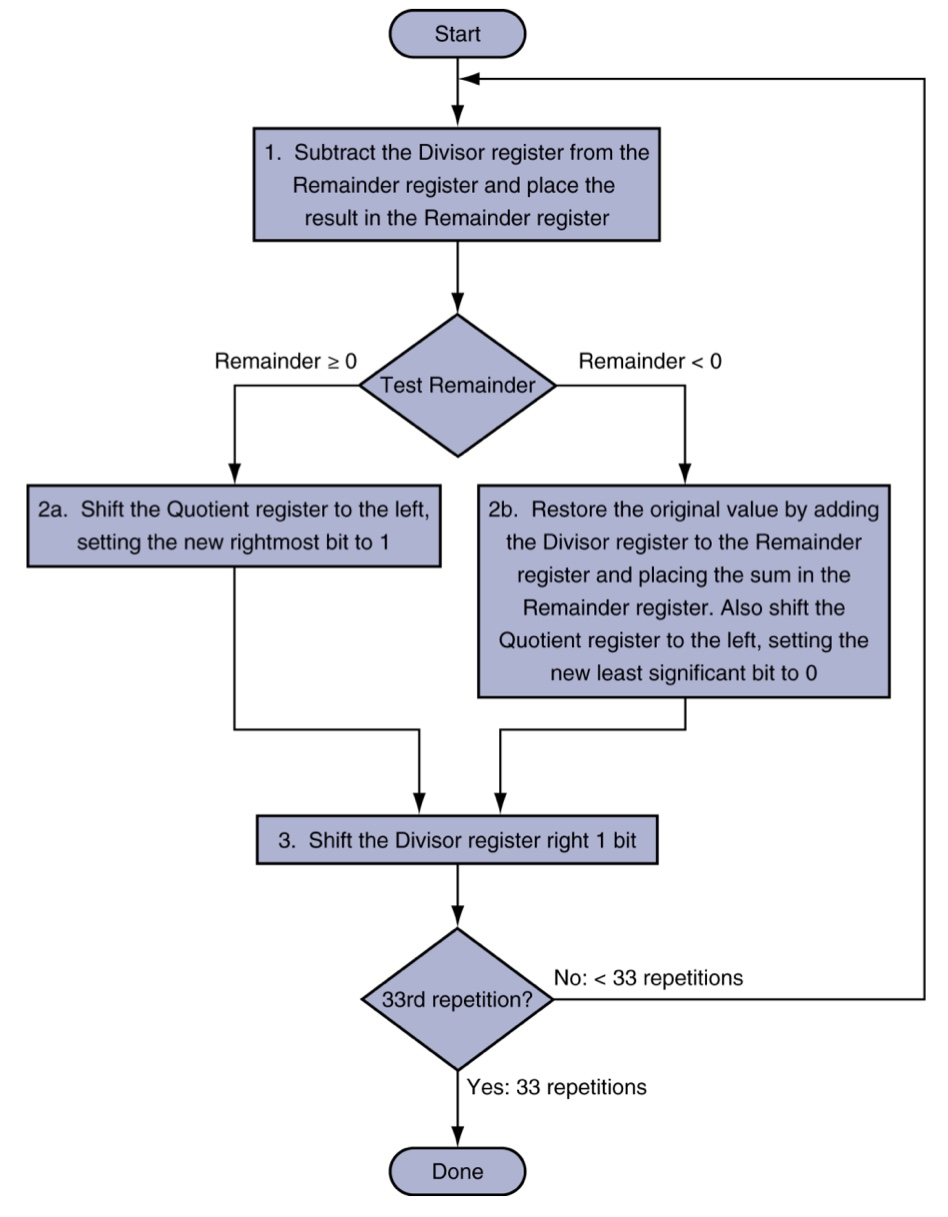
Optimized Divider

곱셈기와 매우 많이 닮았습니다.

하드웨어적으로 양쪽 연산 모두 사용가능합니다.

 

ex) 6(0110) / 2(0010)

4 bit 두 수를 나누는 예시 입니다.

ALU와 divisor 모두 4 bit, dividend는 8 bit

8 bit인 dividend는 상위 4 bit가 remainder(나머지)로, 하위 4 bit가 quotient(몫)로 작동합니다.

(8 bit 레지스터에 초기값이 상위 bit는 0이고 하위는 dividend로 시작)

            remainder        quotient

1) 처음      0000              0110

2) shift      0000              1100

3) sub       1110              1100

4) 복구     0000              1100

5) shift     0001              1000

6) sub      1111              1000

7) 복구     0001             1000

8) shift     0011             0000

9) sub     0001              0001

10) shift   0010             0010

11) sub    0000             0011

4-bit 수의 나눗셈이라, shift/sub가 4단계 일어나면 종료됩니다.

결과는 몫이 0011(3), 나머지는 0

 

Faster Divider

곱셈기 처럼 병렬적인 하드웨어를 사용할 수 없습니다.

나눗셈에서는 remainder에 divisor를 뺀 (subtraction) 결과가 음수인지 아닌지에 따라 다르게 동작하므로

여러개의 하드웨어가 병렬적으로 처리할 수 없습니다.

더 빠른 나눗셈기(SRT division)는 단계 마다 동시에 여러개의 quotient(몫) bit를 구할 수 있습니다.

 

MIPS Division

결과 용으로 HI / LO 2개의 레지스터를 사용합니다.

HI : 32 bit의 remainder (나머지)

LO : 32 bit의 quotient(몫)

 

Instruction

div rs, rt   / divu rs, rt

overflow는 발생하지 않는지, 0으로 나누는지 확인합니다.

필요하다면 소프트웨어 단계에서 체크할 수 도 있습니다.

결과에 접근(access)하기 위해 mifi, mflo를 사용합니다.

 

Floating Point

부동소수점

실수를 표현하는 방법입니다.

 

scientific notation

정수부분이 0이 아니고 일의 자리인 표현을 normalized 표현, 아니면 not normalized 표현입니다.

c언어에서는 float, double 형이 있습니다.

 

IEEE에서 채택한 실수 표현을 주로 사용합니다.

single-precision : 32 bit

double-precision : 64 bit

 

Single-Precision Range (float)

 

exponent 부분에서는 00000001 ~ 11111110 의 범위를 가집니다. (00000000, 11111111은 불가능)

 

가장 작은값

exponent : 00000001 (1) (실제 exponent는 1 - 127 = -126)

fraction : 00000...0000 (사실상 1입니다)

따라서 최솟값은 대략 ±1.0 * 2^(-126) ≒ ±1.2 * 10^-38 입니다.

 

가장 큰 값

exponent : 11111110 (254) (실제 exponent는 254 - 127)

fraction : 1111...1111 (사실상 2입니다.)

따라서 최댓값은 대략 ±2.0 * 2^(127) ≒ ±3.4 * 10^38

 

Double-Precision Range (double)

exponent부분에서는 00000...001 ~ 1111....1110의 범위를 가집니다. (0000....000, 1111...1111은 불가능)

 

가장 작은 값

exponent : 00000000001 (1) (실제 exponent는 1 - 1023 = -1022)

fraction : 0000...0000 (사실상 1입니다.)

따라서 최솟값은 ±1.0 * 2^(-1022) ≒ ±2.2 * 10^-308

가장 큰 값

exponent : 11111111110 (2046) (실제 exponent는  2046 - 1023 = 1023)

fraction : 111..1111 (사실상 2입니다.)

따라서 최댓값은 ±2 * 2^(1023) ≒ ±1.8 * 10^308

 

Floating-Point Precision

실수 표현은 완전 정확한 것이 아닌 최대한 정확하게 맞추는 것입니다.

single(float)에서는 보통 10진법 기준 소수점 6번째까지 정확합니다.

double 에서는 보통 10진법 기준 소수점 16자리까지 정확합니다.

 

Floation-Point Example

-0.75를 표현

-0.75 = (-1)^1 * (2^-1 + 2^-2)

        = (-1)^1 * 0.11

        = (-1)^1 * 1.1 * 2^-1

 

S = 1

Fraction = 100...0000

Exponent = -1 + bias

                (single = -1 + 127 = 126 = 01111110

                 double = -1 + 1023 = 1022 = 01111111110

따라서

single = 1011111101000....0000

double = 101111111110100....000000

---

(float) 110000001010000...0000은 어떤 수인지 구하라

S = 1

Exponent = 10000001 = 129 (실제 exponent = 129 - 127 = 2)

Fraction = 010000...000

 

따라서 (-1)^1 * 1.01 * 2^2

        =(-1)^1 * (1 + 2^-2) * 2^2

        =(-1)^1 * (1.25) * 4

        = -5.0

 

Floating-Point Addition

부동소수점 덧셈

 

ex) (decimal) 9.999 * 10 + 1.610 * 10^-1 을 구하라

1) 소수점 정렬 (작은 수를 큰 수에 맞춥니다)

9.999 * 10 + 0.0161 * 10

2) significand 끼리 더합니다

9.999 + 0.0161 = 10.0151 즉, 10.0151 * 10

3) 결과를 normalize로 바꾸고 overflow나 underflow 검사

1.00151 * 10^2

4) 필요하다면 반올림하거나 renormalize한다

1.002 * 1.^2

 

ex) (binary) 1.000 * 2^-1 + -1.110 * 2^-2 를 구하라 (0.5 + (-0.4375))

1) 소수점 정렬 (작은 수를 큰 수에 맞춥니다)

1.000 * 2^-1 + (-0.1110 * 2^-1)

2) significand 끼리 더합니다.

1.000 * 2^-1 + (-0.1110 * 2^-1) = 0.001 * 2^-1

3) 결과를 normalized하고, overflow나 underflow 검사

0.001 * 2^-1 = 1.000 * 2^-4

4) 필요하다면 반올림하거나 renormalized 한다

1.000 * 2^-4 (no change) = 0.0625

 

FP Adder Hardware

부동 소수점 가산기

integer(정수) adder 보다 훨씬 더 복잡합니다.

한번의 clock cycle 안에 작업을 하기에는 , cycle이 아주 오래 걸리게(느리게) 될 수 있습니다.

느린 clock은 전체 instruction들을 전체적으로 느리게 만듭니다.

따라서 FP adder는 일반적으로 여러번의 cycle로 동작합니다.

pipeline(병렬)화 될 수 있습니다.

하나의 instruction에는 여러 cycycle이 걸리지만 throughput을 높여 여려개의 명령어를 동시에 실행하므로

단위 시간당 FP adder의 가능한 작업의 수는 증가합니다.

FP Arithmetic Hardware

FP multiplier (곱셈기)의 복잡도는 FP adder(가산기)와 비슷합니다.

하지만 adder에서는 significand끼리 더했지만, multiplier는 곱합니다.

 

FP arithmetic 는 보통 다음 기능들을 지원합니다.

addition(덧셈), subtraction(뺄셈), multiplication(곱셈), division(나눗셈), reciprocal(역수, 분모), squareroot(제곱), ...

FP ↔ integer 변환 (conversion)

 

FP operation은 일반적으로 여러번의 cycle로 동작합니다.pipeline(병렬)화 될 수 있습니다.

 

FP Instruction in MIPS

FP hardware(FP ALU)는 ISA를 확장하는 coprocessor입니다.Flotion point 연산을 위해 추가적인 instruction set과 추가적인 register가 존재합니다.

 

FP data를 담는 32개의 FP 레지스터가 존재합니다.따라서 32 bit MIPS의 총 레지스터는 64개가 됩니다.

 

single precision(float)는 하나의 register를 사용합니다.$f0, $f1, $f2, ....$f31double precision(double)은 2개의 register을 묶어서 한 쌍으로 사용합니다.$f0/$f1, $f2/$f3, ....

 

FP instruction은 오직 FP register만을 사용합니다.따라서 opcode를 보고 어떤 register을 사용할 지 결정할 수 있습니다.이를 통해 register를 구분하기 위한 register operand의 bit 수가 늘어날 필요는 없습니다.opcode를 보고 register을 구분함으로써 5개의 bit만으로도 register을 판별할 수 있는 것입니다.

 

FP instruction을 위한 별도의 instruction이 있습니다.FP instruction은 FP register만을 이용합니다.1) Load / Store

• sigle precision : lw1, swc1 (ex : lwc1 $f8, 32($sp)
• double precision : ldc1, sdc1 

2) Arithmetic

• single precision : add.s, sub.s, mul.s, div.s (ex : add.s $f0, $f1, $f6)
• double precision : add.d, sub.d, mul.d, div.d (ex : mul.d $f4, $f4, $f6)

3) Comparison

• single and double : c.xx.s, c.xx.d (xx는 eq, lt, le, ....)                                                                                  ex) c.lt.s $f3, $f4

4) Branch on FP condition code true or false

• bc1t, bc1f (ex : bc1t TargetLabel

FP Example : ℉ to ℃

화씨 에서 섭씨로 변환

c code

float f2c(float fahr){
   return ((5.0 / 9.0) * (fahr - 32.0));
}

fahr = $f12, result = $f0 전역변수로 설정

 

compiled MIPS code

 

Accurate Arithmetic

부동 소수점의 정확한 연산을 위해 IEEE Std 754는 additional rounding control을 제공합니다.

guard, round, stick 3개의 bit를 이용해 반올림의 정확성을 높히는 것입니다.

또한 rounding mode 도 존재합니다. 종류에는 up, down, truncate, nearest even, away from, 0 등이 있어

사용자에 따라 선택가능합니다.

부동 소수점은 매우 큰 수를 표현할 수 있지만 오류가 존재합니다.

예를 들어 컴퓨터 상에서 (1.5 * 10^32 +1) - 1.5*10^32의 결과는 1이 아니라 0입니다.

반면에 (1.5 * 10^32 - 1.5 * 10^32) +1은 정상적으로 1입니다.

이렇게 같은 식에도 답이 다르게 나오는 이유는 컴퓨터가 매우 큰 수와 매우 작은 수를 함께 처리할 수 없기 때문

입니다. 개발을 할 때 매우 큰 숫자와 매우 작은 숫자를 함께 사용하는 것은 지양해야합니다.

 

Subword Parallellism

멀티미디어 (그래픽, 오디오)는 주로 8 bit, 16 bit의 짧은 데이터가 매우 많이 연결되어있습니다.

따라서 동시에 빨리 처리하는것이 필요합니다.

예를들어 128 bit adder을 여러개의 작은 adder로 사용해 데이터 연산 처리를 병렬로 처리합니다.

병렬로 처리하면서 동시에 수행할 수 있기 때문에 처리 속도가 빨라집니다.

128 = 16 * 8 bit adder

128 = 8 * 16 bit adder

128 = 4 * 32 bit adder

이러한 partitioned carry chain으로 adder를 사용해 병렬로 처리하는 것은 subword parpallelism이라고 합니다.

다음과 같이 불리기도 합니다. DLP, Vector parallelism, SIMD

 

Right Shift and Division

left shift는 보통 2를 제곱해줍니다. ( << )

right shift는 보통 2를 제곱해 나누어 줍니다. ( >> ) 하지만 unsigned integer에만 적용됩니다.

그럼 signed integer 에서 right shift는 어떻게 될까?

 

signed integer에서 right shift는 부호 bit를 그만큼 복사해줍니다.

ex) -5 / 4

11111011 >> 2 = 11111110 = -2

 

Associativity

병렬 프로그램은 예기치 못한 순서로 작업을 할 수 있습니다.

예를 들어 x+y+x의 연산에서 (x+y)+z와 x+(y+z)의 연산결과는 달라질 수 있습니다.

FP 연산이 근사계산이기 때문입니다.

그리고 컴파일러 마다 연산하는 순서가 다르기 때문에 발생합니다.

위에 표를 보면 (x+y)를 먼저하면 1이 나오지만 (y+z)를 먼저하면 0이 나옵니다.

 

x + (y + z)에서 y+z을 계산한 결과의 fraction이 23bit을 넘어서기 때문입니다.

따라서 fraction은 23 bit에서 잘리고, 잘릴 때 버림 혹은 반올림이 됩니다.